A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
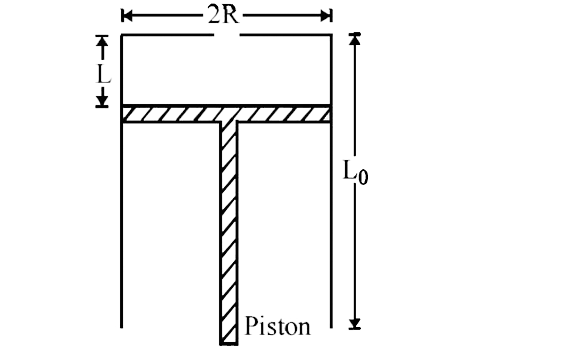
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
(2P0πR2πR2P0+Mg)(2L)
(P0πR2−MgπR2P0)(2L)
(P0πR2+MgπR2P0)(2L)
(P0πR2πR2P0−Mg)(2L)
The correct Answer is:D
The condition for equlibrium of the piston is
Mg=(P0−p)πR2
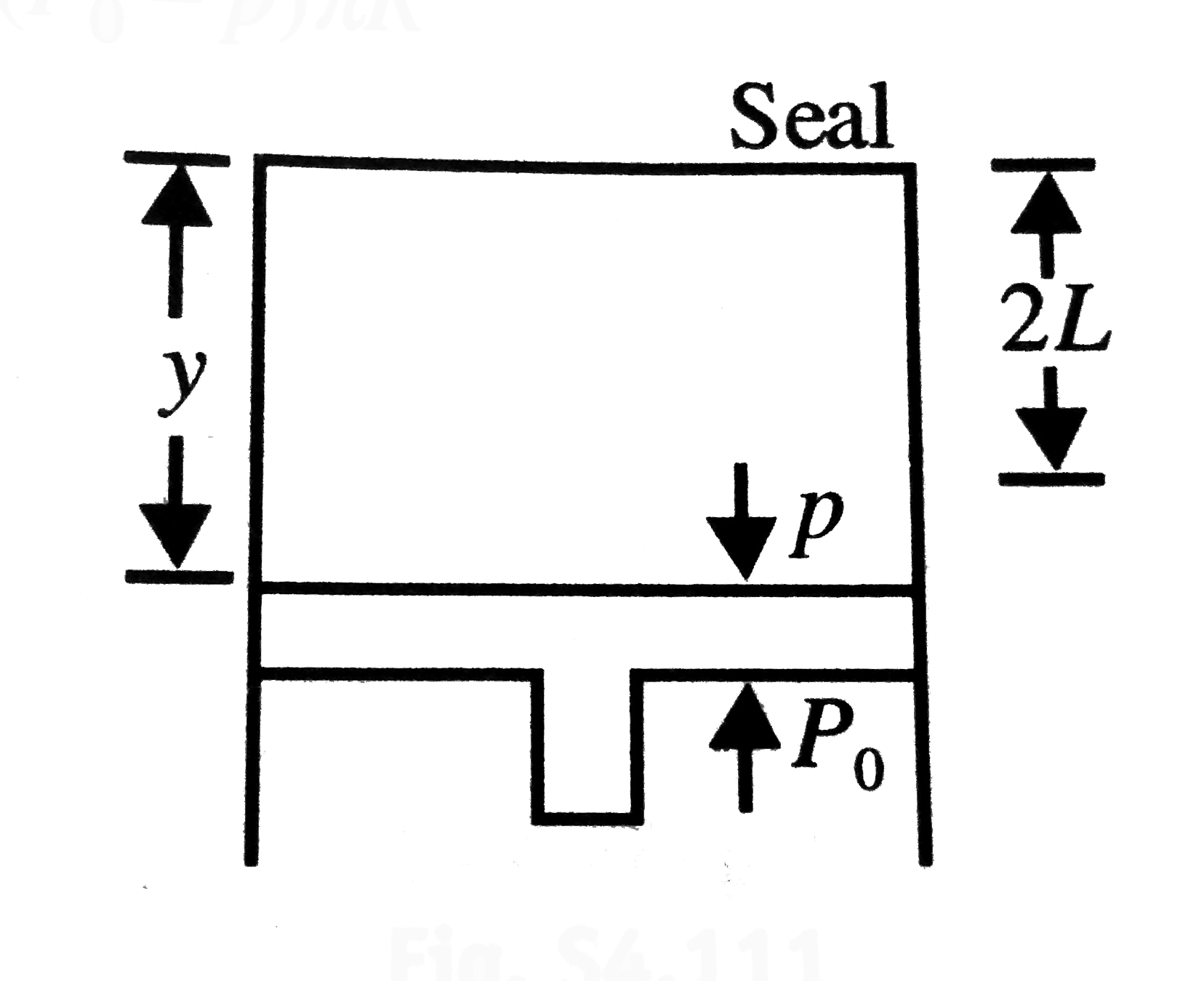
p=−MgπR2+P0
Since the cylinder is thermally conducting the temperature remain the same.
Therefore P0×(2L×πR2)=py×πR2
y=P0×(2L)=P0[P0=Mgπr2]×2L
=P0×πr2p0πR2−Mg×2L
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Video
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - MCQ_TYPE
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at the bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
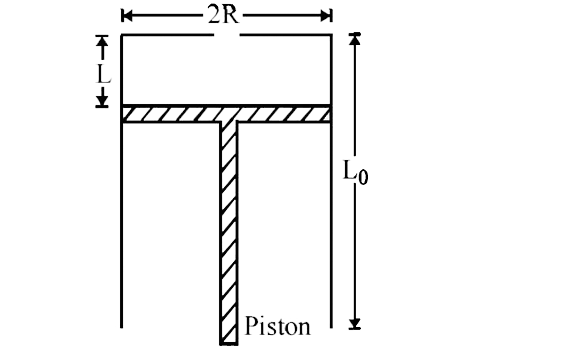
The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
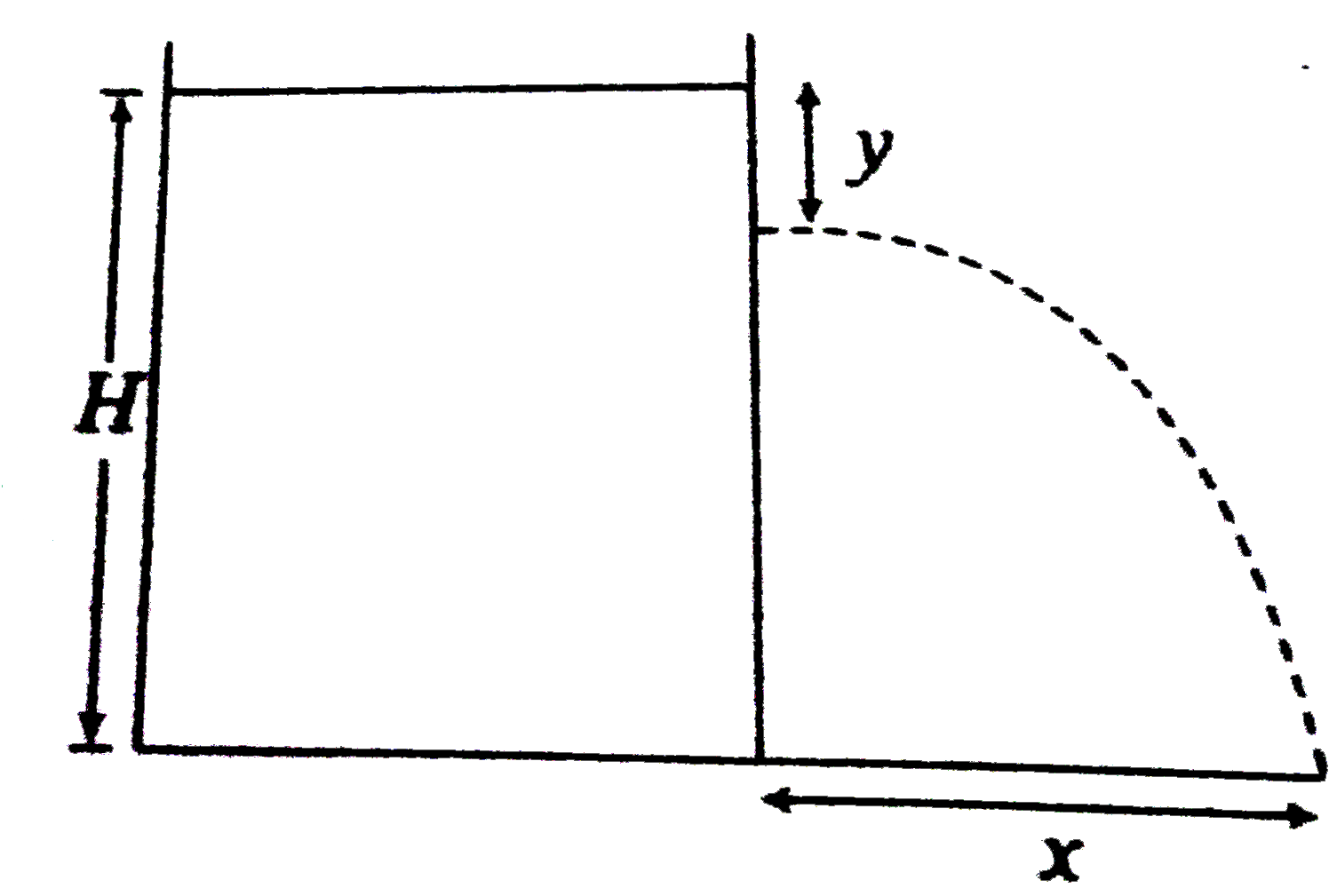
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA light rod of length l is pivoted at distance l/4 from the left end and has two masses m0 and m attached to its ends such that rod is in equilibrium. Find m in terms of m0.

View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View SolutionFrom the top of aspier the angle of depression of the top and bottom of a tower of height h are θ and ϕ respectively. Then height of the spier and its horizontal distance from the tower are respectively.
View SolutionA very long, solid insulating cylinder with radius R has a cylindrical hole with radius a bored along its entire length. The axis of the hole is at a distance b from the axis of the cylinder, where a<b<R (as shown in figure). The solid material of the cylinder has a uniform volume charge density ρ. Find the magnitude and direction of the electric field inside the hole, and show that this is uniform over the entire hole.
 .
.
View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View Solution