A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
−k2a
−ka
−2ka
−ak
The correct Answer is:A
To find the work done by the force F=−kx2 when displacing a particle from x=+a to x=2a, we will follow these steps:
Step 1: Understand the Work Done by a Variable Force
The work done W by a variable force when moving from position x1 to x2 is given by the integral:
W=∫x2x1Fdx
In our case, F=−kx2, x1=a, and x2=2a.
Step 2: Set Up the Integral
Substituting the values into the work integral, we have:
W=∫2aa−kx2dx
Step 3: Evaluate the Integral
To evaluate the integral, we can rewrite it as:
W=−k∫2aa1x2dx
The integral of 1x2 is −1x. Thus, we can evaluate it as follows:
W=−k(−1x)2aa=−k(−12a+1a)
Step 4: Simplify the Expression
Now, simplifying the expression:
W=−k(1a−12a)=−k(22a−12a)=−k(12a)
Thus, we have:
W=−k2a
Final Answer
The work done by the force in displacing the particle from x=+a to x=2a is:
W=−k2a
---
The work done W by a variable force when moving from position x1 to x2 is given by the integral:
W=∫x2x1Fdx
In our case, F=−kx2, x1=a, and x2=2a.
Substituting the values into the work integral, we have:
W=∫2aa−kx2dx
To evaluate the integral, we can rewrite it as:
W=−k∫2aa1x2dx
The integral of 1x2 is −1x. Thus, we can evaluate it as follows:
W=−k(−1x)2aa=−k(−12a+1a)
Now, simplifying the expression:
W=−k(1a−12a)=−k(22a−12a)=−k(12a)
Thus, we have:
W=−k2a
The work done by the force in displacing the particle from x=+a to x=2a is:
W=−k2a
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Solved Examples
12 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View Solution
Knowledge Check
A force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
A2.1JB2.5JC3.5JD4.5JA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
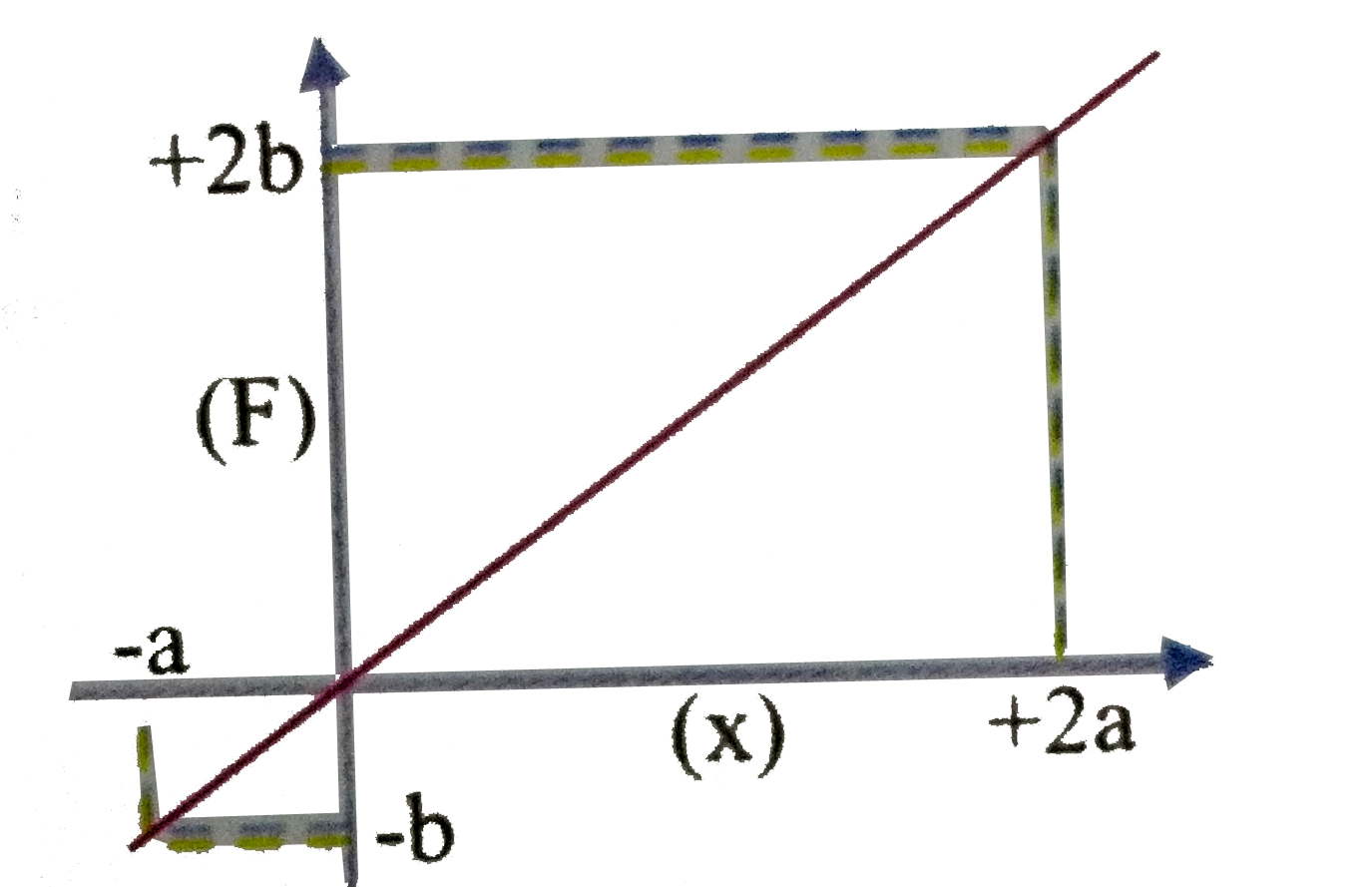 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24abA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 JB80 JC64 JD52 J
A force F=(a+bx) acts on a particle in x direction where a and b are constants . Find the work done by this force during displacement from x1 to x2 .
View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=a+b x acts on a particle in the X-direction, where a and b are constants. Find the work done by this force during a displacement from x=0 to x=d/
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View Solution
