A force of 75 N is applied to a block of mass 25 kg, resting on a smooth horizontal surface. In how much time, the block will acquire a speed of 12 m/s?
1 sec
2sec
4 sec
8 sec
The correct Answer is:C
To solve the problem, we will use Newton's second law of motion and the concept of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Given Information
- Force (F) = 75 N
- Mass (m) = 25 kg
- Final speed (v) = 12 m/s
- Initial speed (u) = 0 m/s (since the block is at rest)
Step 2: Calculate the Change in Momentum
Momentum (p) is defined as the product of mass and velocity.
- Initial momentum (p_initial) = m * u = 25 kg * 0 m/s = 0 kg·m/s
- Final momentum (p_final) = m * v = 25 kg * 12 m/s = 300 kg·m/s
Now, we can find the change in momentum (Δp):
Δp=pfinal−pinitial=300kg⋅m/s−0kg⋅m/s=300kg⋅m/s
Step 3: Apply Newton's Second Law
According to Newton's second law:
F=ΔpΔt
Where:
- F is the force applied
- Δp is the change in momentum
- Δt is the time taken
Rearranging the formula to find Δt:
Δt=ΔpF
Step 4: Substitute the Values
Now we can substitute the values we have:
Δt=300kg⋅m/s75N
Step 5: Calculate Δt
Calculating the above expression:
Δt=30075=4 seconds
Conclusion
The block will acquire a speed of 12 m/s in 4 seconds.
---
- Force (F) = 75 N
- Mass (m) = 25 kg
- Final speed (v) = 12 m/s
- Initial speed (u) = 0 m/s (since the block is at rest)
Momentum (p) is defined as the product of mass and velocity.
- Initial momentum (p_initial) = m * u = 25 kg * 0 m/s = 0 kg·m/s
- Final momentum (p_final) = m * v = 25 kg * 12 m/s = 300 kg·m/s
Δp=pfinal−pinitial=300kg⋅m/s−0kg⋅m/s=300kg⋅m/s
According to Newton's second law:
F=ΔpΔt
Where:
- F is the force applied
- Δp is the change in momentum
- Δt is the time taken
Δt=ΔpF
Now we can substitute the values we have:
Δt=300kg⋅m/s75N
Calculating the above expression:
Δt=30075=4 seconds
The block will acquire a speed of 12 m/s in 4 seconds.
Topper's Solved these Questions
Similar Questions
A pull of 15 N is applied to a rope attached to a block of mass 7 kg lying on a smooth horizontal surface. The mass of the rope is 0.5 kg. What is the force exerted by the block on the rope?
View SolutionA force of 50 N acts in the direction as shown in figure. The block of mass 5kg. Resting on a smooth horizonatal surface. Find out the acceleration of the block.
View Solution
Knowledge Check
A horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
A15.5 NB10.3 NC8.5 ND19.2 NA horizontal force of 20 N i sapplied to a block of mass 4 kg resting on a rough horiozontal table. If the blcok does not move on the table, how much fricrtional force the table is applying on the blockgt What can be said about the coefficient of static friction between the block and the table? Takeg=ms2.
A-20 N , greater than 0.5B-20 N , less than 0.5C-40 N , greater than 0.5D-50 N , equal to 0.5A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
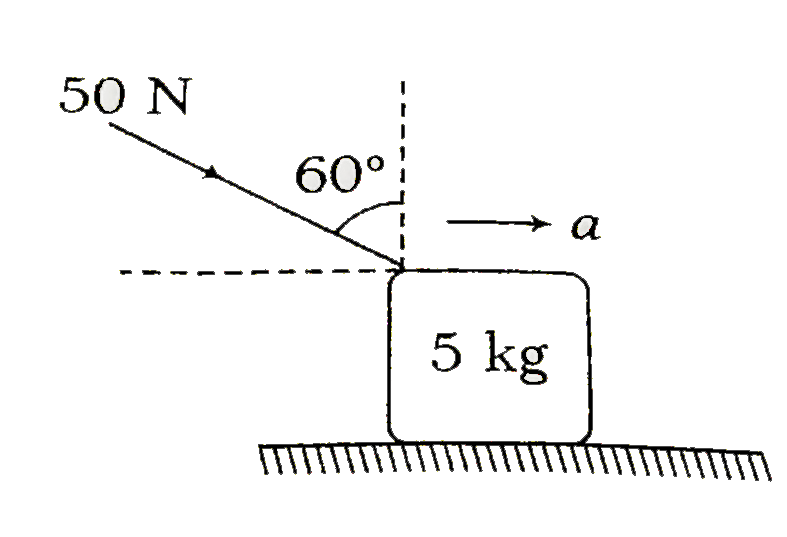 A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionA force of 1000 N is applied on a body of mass 100 kg moving with a velocity of 5m/s. How much time does it require to acquire a velocity of 25m/s ?
View SolutionA force of 100 N acts in the direction as shown in figure on a block of mass 10 kg resting on a smooth horizontal table. The speed acquired by the block after it has .moved a distance of 10 m, will be - (in m/sec) (g=10m/sec2)

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA constant force of 5 N is applied on a block of mass 20 kg for a distance 2 0 m. The kinetic energy acquired by the block is
View Solution
