A force →F(yˆl+xˆJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
Step by step video & image solution for A force vecF(yhatl+xhatJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - SL ARORACHAPTER - WORK, POWER AND ENERGYEXERCISE - PROBLEM
14 Videos
- WORK, POWER AND ENERGYBOOK - SL ARORACHAPTER - WORK, POWER AND ENERGYEXERCISE - Problem for Self Practice
12 Videos
- WORK, POWER AND ENERGYBOOK - SL ARORACHAPTER - WORK, POWER AND ENERGYEXERCISE - Type F
15 Videos
- Work, Energy and powerBOOK - SL ARORACHAPTER - Work, Energy and powerEXERCISE - EXERCISE
415 Videos
Similar Questions
A force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
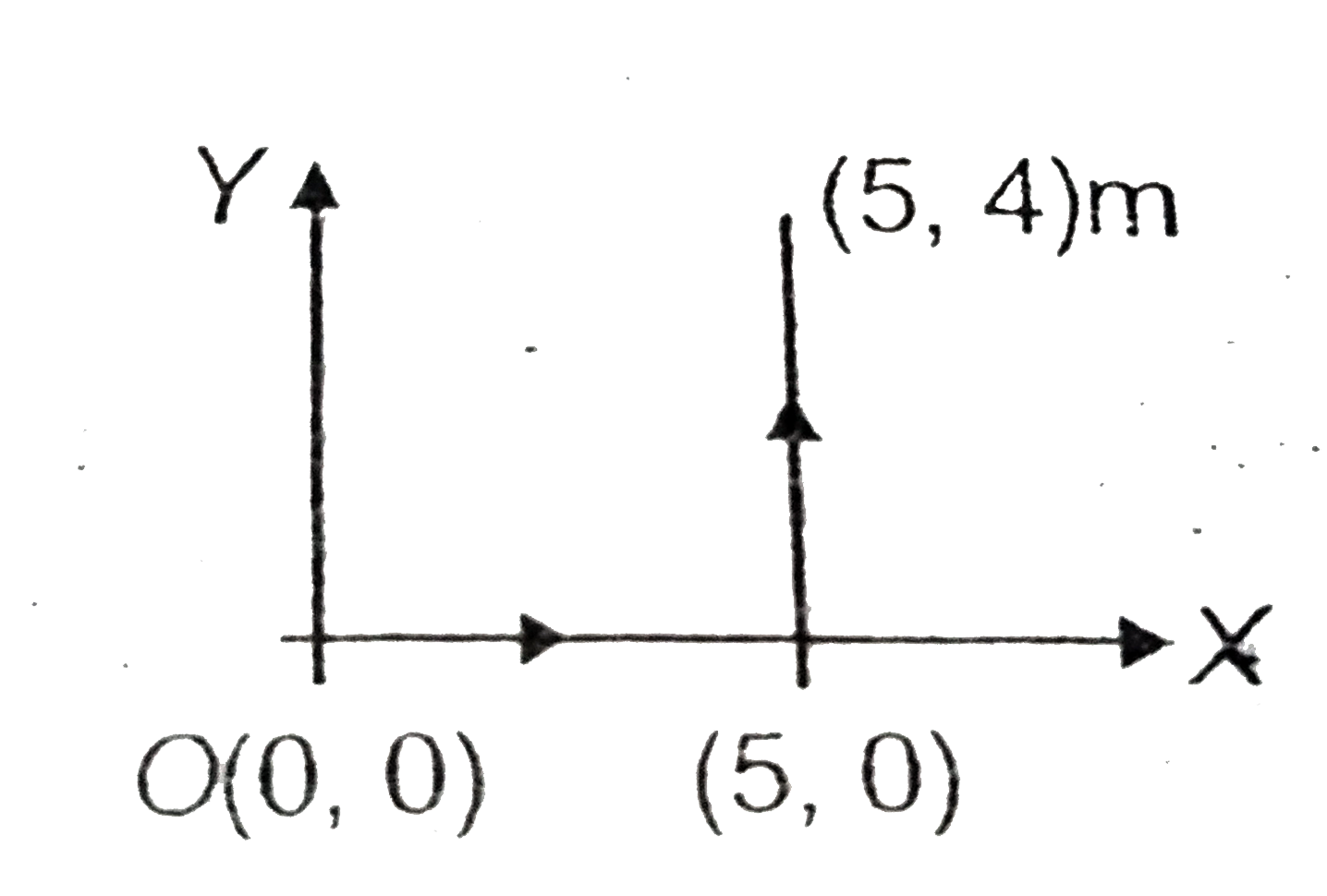
View Solution
Knowledge Check
A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionA force F=−K(yˆi+xˆj), acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a, a). The total work done by the force is
View SolutionA force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
View SolutionA force →F=k[yˆi+xˆj] where k is a positive constant acts on a particle moving in x-y plane starting from the point (3, 5), the particle is taken along a straight line to (5, 7). The work done by the force is :
View SolutionA force →F=(3→i+4→j)N, acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is
(##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">
View Solution
