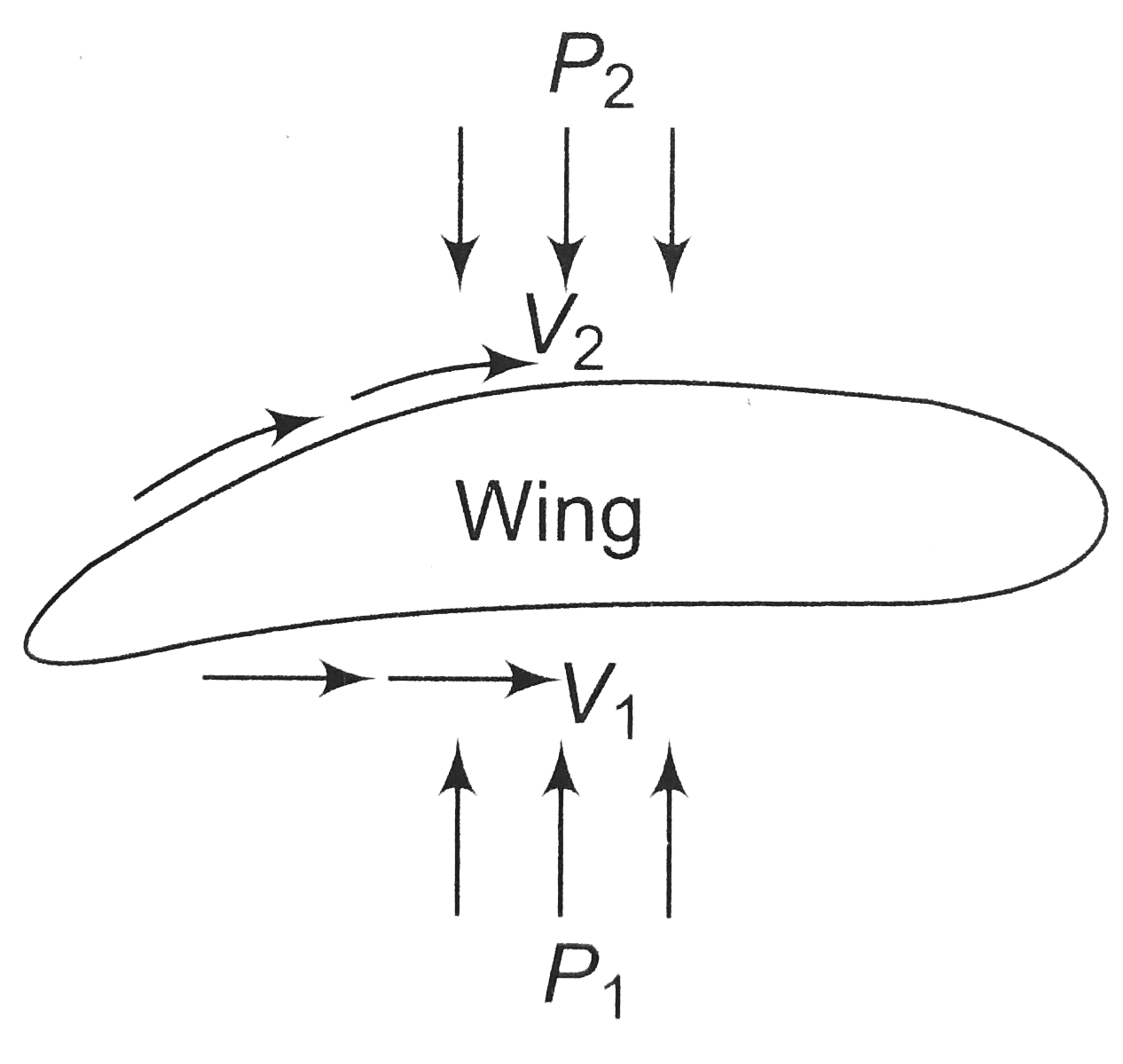
A fully loaded Boeing aircraft has a mass of 3.3×105kg. Its total wing area is 500m2 . It is in level flight with a speed of 960km/h.
(a) Estimate the pressure difference between the lower and upper surfaces of the wings
(b) Estimate the fractional increases in the speed of the air on the upper surfaces of the wing relative to the lower surface. The density of air is 1.2kg/m3.
(a). The weighht of the boeing aircraft is balanced by the upward force due to the pressure difference
ΔP×A=3.3×105kg×9.8
ΔP=(3.3×105kg×9.8ms−2)/500m2
6.5×103Nm−2
(b). We ignore the small height difference between the top and bottom sides in eQ. The pressure difference between them is then
ΔP=ρ2(v22−v21)
When v2 is the speed of air over the upper surface and v1 is the speed under the bottom surface.
(v2−v1)=2ΔPρ(v2+v1)
Taking the average speed
vav=(v2+v1)/2=960km/h=267ms−1
We have
v2−v1vav=ΔPρv2av≈0.08
the speed above the wing needs to be only 8% higher than that below.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- LAWS OF MOTION BOOK - NCERT ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EXERCISE
40 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
Similar Questions
An aeroplane of mass 3×104kg and total wing area of 120 m2 is in a level flight at some height the difference in pressure between the upper and lower surfaces of its wings in kilo pascal is (g=10m/s2)
View SolutionStomata are distributed more on the lower surface than on the upper surface in
View Solution
Knowledge Check
An aircraft of mass 4×105kg with total wing area 500m2 in level flight at a speed of 720 kmh−1. The density of a at its height is 1.2kgm−3. The fractional increases in the speed of the air on the upper surface of its wings relative to the lower surface is (take g=10ms−2)
A0.04B0.08C0.17D0.34A plane is in level flight at constant speed and each of its two wings has an area of 25m2 . If the speed of the air on the upper and lower surfaces of the wing are 270kmh−1 and '234 km h^(-1)' respectively, then the mass of the plane is (Take the density of the air =1kgm−3)
A1550 kgB1750 kgC3500 kgD3200 kg
The rms speed of helium on the surface of the sun is 6.01km/s. Make an estimate of the surface temperature of the sun.
View SolutionThe speed of flow past the lower surface of a wing of an aeroplane is 50ms−1. What speed of flow over the upper surface will give a dynamic lift of 1000pa? Density of air =1.3kgm−3
View SolutionThe upper surface of wings of an aeroplane are made convex and lower concave downwards?
View SolutionAir is streaming past a horizontal airplane wing such that its speed is 90ms−1 at the lower surface and 120ms−1 over the upper surface. if the wing is 10m long and has an average width of 2m, the difference of pressure on the two sides and the gross lift on the wing respectively, are (density of air =1.3kgm−3)
View SolutionA force Fis tangentially applied on the upper face of a cube of side b and whose lower face is fixed. If modulus of rigidity is n then upper surface of cube is shifted to
View SolutionState whether true or false. Rewrite the false statements in their correct form :
Transpiration is more from the upper surface of a leaf as compared to lower surface in a dorsiventral leaf.
View Solution
