A gardener holds a pipe of inside cross-sectional area 3.60cm2 at a height of 1.50m from ground. The opening at the nozzle of pipe has cross-sectional area 0.250cm2. Water velocity in the segment of the hose that lies on the ground is 50.0cm/s. a. What is the velocity of water leaving the nozzle? b. What is the thrust force experienced by the gardener due to flow of water through nozzle. c. What is the water pressure in the hose on the ground?
To solve the problem step by step, we will address each part of the question systematically.
Given Data:
- Cross-sectional area of the pipe, A1=3.60cm2=3.60×10−4m2
- Cross-sectional area of the nozzle, A2=0.250cm2=0.250×10−4m2
- Velocity of water in the hose on the ground, V1=50.0cm/s=0.50m/s
- Height of the nozzle from the ground, h=1.50m
- Density of water, ρ=1000kg/m3
Part (a): Velocity of Water Leaving the Nozzle
Using the principle of conservation of mass (continuity equation), the volume flow rate must be constant throughout the pipe and nozzle:
A1V1=A2V2
Rearranging for V2:
V2=A1V1A2
Substituting the values:
V2=(3.60×10−4m2)(0.50m/s)0.250×10−4m2
Calculating V2:
V2=1.80×10−40.250×10−4=7.2m/s
Part (b): Thrust Force Experienced by the Gardener
The thrust force F can be calculated using the change in momentum per unit time (rate of momentum flow):
F=˙mV2
Where ˙m is the mass flow rate given by:
˙m=ρA2V2
Substituting the values:
˙m=1000kg/m3×(0.250×10−4m2)×(7.2m/s)
Calculating ˙m:
˙m=1000×0.250×10−4×7.2=1.8kg/s
Now substituting ˙m into the thrust force equation:
F=1.8kg/s×7.2m/s=12.96N≈13N
Part (c): Water Pressure in the Hose on the Ground
Using Bernoulli's equation, we can find the pressure at the ground level:
P1+12ρV21+ρgh=P2+12ρV22
Assuming P2 is atmospheric pressure (approximately 101325Pa), we can rearrange to find P1:
P1=P2+12ρV22−12ρV21−ρgh
Substituting the values:
P1=101325+12×1000×(7.2)2−12×1000×(0.5)2−1000×9.81×1.5
Calculating each term:
1. 12×1000×(7.2)2=25920Pa
2. 12×1000×(0.5)2=125Pa
3. 1000×9.81×1.5=14715Pa
Now substituting back:
P1=101325+25920−125−14715
Calculating P1:
P1=101325+25920−125−14715=101325+25920−14840=101325+11080=112405Pa
Summary of Answers:
- (a) Velocity of water leaving the nozzle, V2=7.2m/s
- (b) Thrust force experienced by the gardener, F≈13N
- (c) Water pressure in the hose on the ground, P1≈112405Pa
- Cross-sectional area of the pipe, A1=3.60cm2=3.60×10−4m2
- Cross-sectional area of the nozzle, A2=0.250cm2=0.250×10−4m2
- Velocity of water in the hose on the ground, V1=50.0cm/s=0.50m/s
- Height of the nozzle from the ground, h=1.50m
- Density of water, ρ=1000kg/m3
2. 12×1000×(0.5)2=125Pa
3. 1000×9.81×1.5=14715Pa
- (a) Velocity of water leaving the nozzle, V2=7.2m/s
- (b) Thrust force experienced by the gardener, F≈13N
- (c) Water pressure in the hose on the ground, P1≈112405Pa
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Exercise 4.3
Explore 10 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
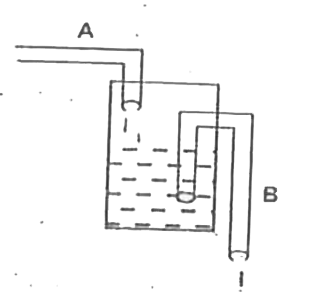
The velocity of the water flowing from the inlet pipe is less than the velocity of water flowing out from the spin pipe B. Then
View SolutionA lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mH
Water is discharged from a pipe of cross-section area 3.2cm2 at the speed of 5m//s. Calculate the volume of water discharged:
in cm3 per sec
View SolutionA hose-pipe of cross-section area 2cm2 delivers 1500 litres of water in 5 minutes. What is the speed of water in m/s through the pipe?
View SolutionWater is discharged from a pipe of cross-section area 3.2cm2 at the speed of 5m//s. Calculate the volume of water discharged:
in litres per minute.
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionWater is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View SolutionHow many litres of water flow out of a pipe having an area of cross-section of 5 cm2 in one minute, if the speed of water in the pipe is 30 cm/sec ?
View Solution
