A gas expands with temperature according to the relation . What is the work done when the temperature changes by ?
The correct Answer is:B
To find the work done when the temperature of a gas changes by 30∘C and the volume expands according to the relation V=kT2/3, we can follow these steps:
Step 1: Understand the Relation
The volume V of the gas is given by the equation:
V=kT2/3
where k is a constant and T is the temperature in Kelvin.
Step 2: Differentiate the Volume
To find the change in volume dV with respect to temperature dT, we differentiate the volume equation:
dV=ddT(kT2/3)=k⋅23T−1/3dT
Step 3: Use the Ideal Gas Law
From the ideal gas law, we know:
PV=nRT
We can express pressure P in terms of T and V:
P=nRTV
Substituting V=kT2/3 into the equation gives:
P=nRTkT2/3=nRkT1/3
Step 4: Set Up the Work Integral
The work done W during the expansion can be expressed as:
W=∫PdV
Substituting the expressions for P and dV:
W=∫(nRkT1/3)(k⋅23T−1/3dT)
This simplifies to:
W=∫nRk⋅k⋅23T1/3T−1/3dT=∫2nR3dT
Step 5: Evaluate the Integral
The integral becomes:
W=2nR3∫dT=2nR3(T2−T1)
Given that the temperature change is 30∘C (or 30K):
W=2nR3⋅30=20nR
Step 6: Final Result
Assuming we have 1 mole of gas (n=1):
W=20R
Conclusion
Thus, the work done when the temperature changes by 30∘C is:
W=20R
The volume V of the gas is given by the equation:
V=kT2/3
where k is a constant and T is the temperature in Kelvin.
To find the change in volume dV with respect to temperature dT, we differentiate the volume equation:
dV=ddT(kT2/3)=k⋅23T−1/3dT
From the ideal gas law, we know:
PV=nRT
We can express pressure P in terms of T and V:
P=nRTV
Substituting V=kT2/3 into the equation gives:
P=nRTkT2/3=nRkT1/3
The work done W during the expansion can be expressed as:
W=∫PdV
Substituting the expressions for P and dV:
W=∫(nRkT1/3)(k⋅23T−1/3dT)
This simplifies to:
W=∫nRk⋅k⋅23T1/3T−1/3dT=∫2nR3dT
The integral becomes:
W=2nR3∫dT=2nR3(T2−T1)
Given that the temperature change is 30∘C (or 30K):
W=2nR3⋅30=20nR
Assuming we have 1 mole of gas (n=1):
W=20R
Thus, the work done when the temperature changes by 30∘C is:
W=20R
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 9
3 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 10
3 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 7
3 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
Similar Questions
One mole of a gas expands with temperature T such thaht its volume, V=KT2, where K is a constant. If the temperature of the gas changes by 60∘C then the work done by the gas is
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View Solution
Knowledge Check
A gas expands with temperature according to the relation V=KT23.Work done when the temperature changes by 60K is.
A10RB30RC40RD20RRatio of CP and Cv depends upon temperature according to the following relation
Aγα TBγα1/TCγα√TDγαTo
If gas expands according to relation P = 4 V, then work done in expansion Vo to 3Vo
View SolutionAn ideal gas mixture filled inside a balloon expands according to the relation PV2/3= constant. What will be the temperature inside the balloon
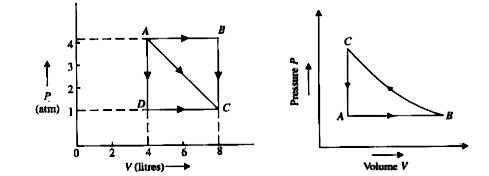
View SolutionA gas expands from A to C along three different paths as shown in Fig. What is the work done by the gas along the path ABC, AC and ADC?
View SolutionPressure P, Volume V and temperature T of a certain material are related by the P=αT2V. Here α is constant. Work done by the material when temparature changes from T0 to 2T0 while pressure remains constant is :
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View Solution
