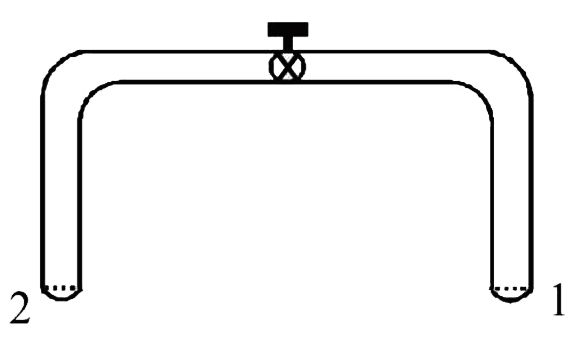
A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
Air from end 1 flows towards end 2. There is no change in the volume of the soap bubble.
Air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases.
No change occurs.
Air from end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.
The correct Answer is:B
△p1=4Tr1 and △p2=4Tr2
r1<r2∴△p1>△p2
Therefore air will flow from 1 to 2 and volume of bubble at end 1 will increase.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - LC_TYPE
3 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Fill In The Blanks
1 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
Knowledge Check
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.
 Aair from end 1 flows towards 2. No change in the volume of the soap bubblesBair from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesCno change occursDair form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.
Aair from end 1 flows towards 2. No change in the volume of the soap bubblesBair from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesCno change occursDair form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.Two spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
AR=r1+r2BR=(r1+r2)12CR=√r21+r22DR=[(r2r2(r1+r2)]An isolated and charged spherical soap bubble has a radius 'r' and the pressure inside is atmospheric. If 'T' is the surface tension of soap solution, then charge on drop is:
A2√2rTε0B8πr√2rTε0C8πr√rTε0D8πr√2rTε0
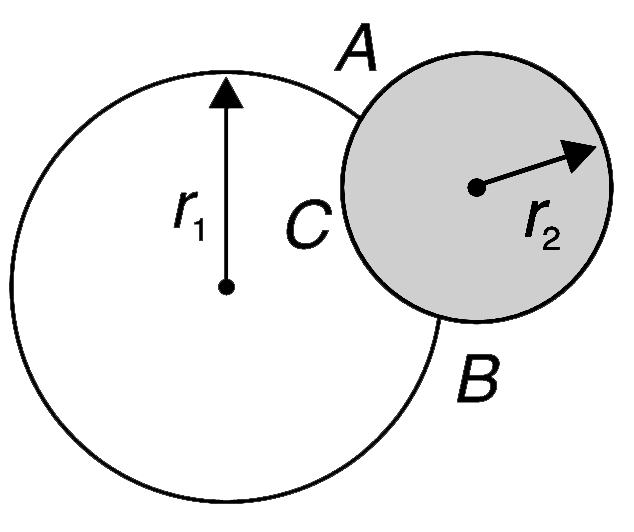
Two soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionTwo spherical soap bubbles of a radii 1 cm and 2 cm vacuum coalesce under isothermal conditions . The resultant bubble has a radius of
View SolutionA soap bubble A of radius 0.03 m and another bubble B of radius 0.04 m are brought together, so that the combined bubble has a common interface of radius r, then the value of r is
View SolutionTwo unequal soap bubbles are formed one on each side of a tube closed in the middle by a tap. What happens when the tap is opened to put the two bubbles in communication?
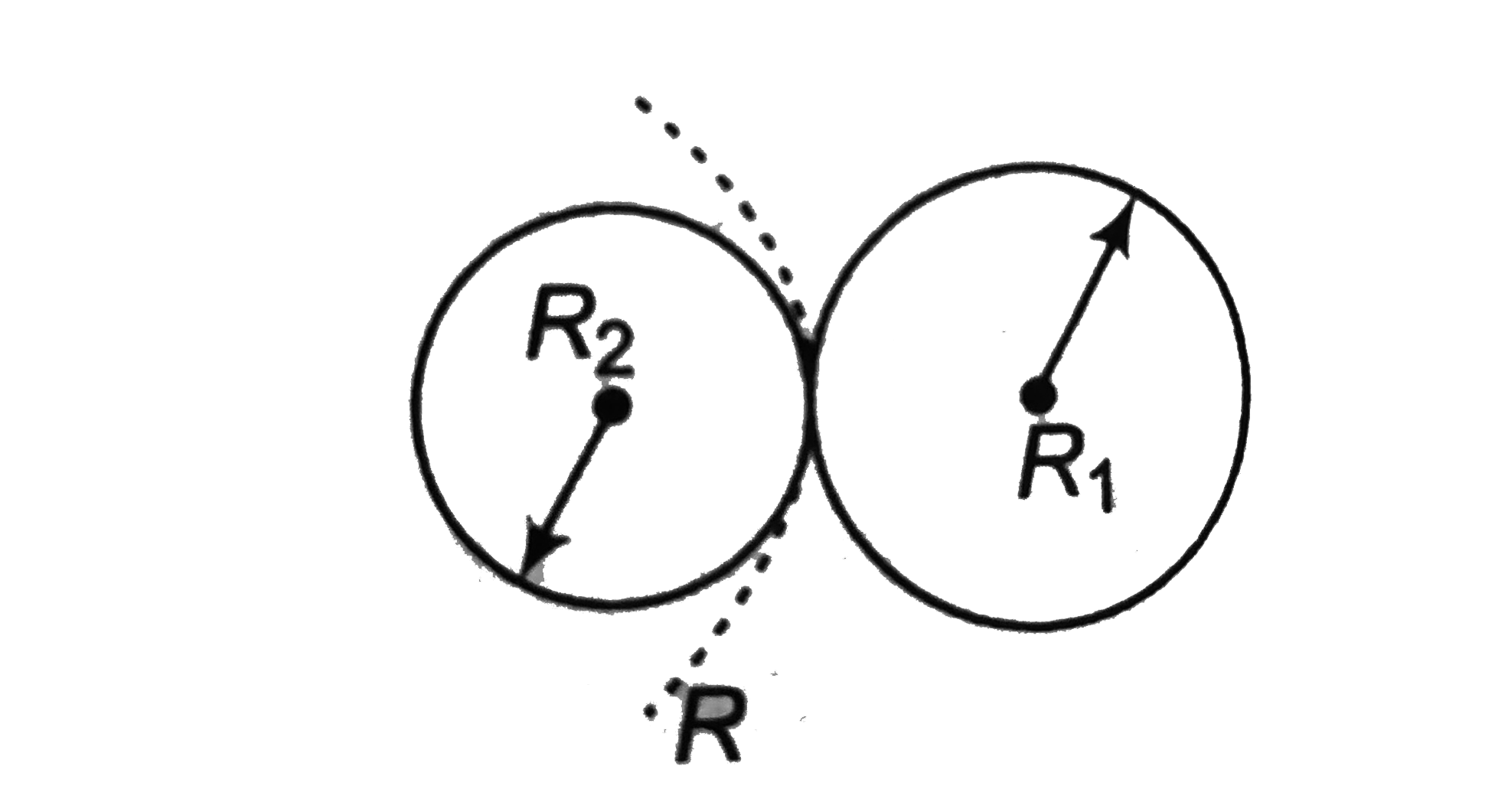
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
 .
.
View Solution