A gun is fired from a moving platform and ranges of the shot are observed to be R1andR2 when the platform is moving forwards and backwards, respectively, with velocity vP. Find the elevation of the gun ∝ in terms of the given quantities.
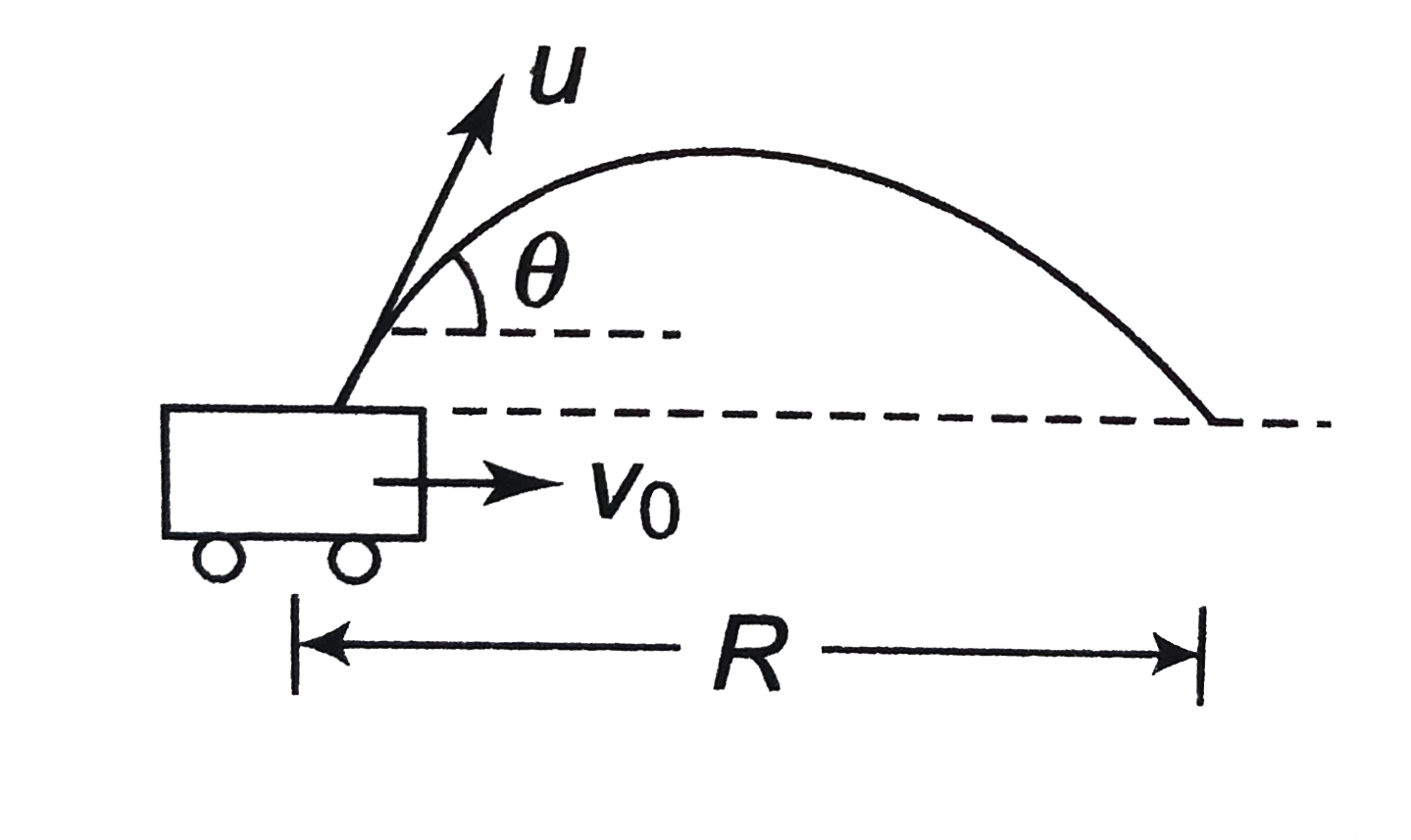
For projectile:
Horizontal component =ucosθ+v0
vertical component =usinθ
T=2usinθg........(i)
R=(ucosθ+v0)T........(ii)
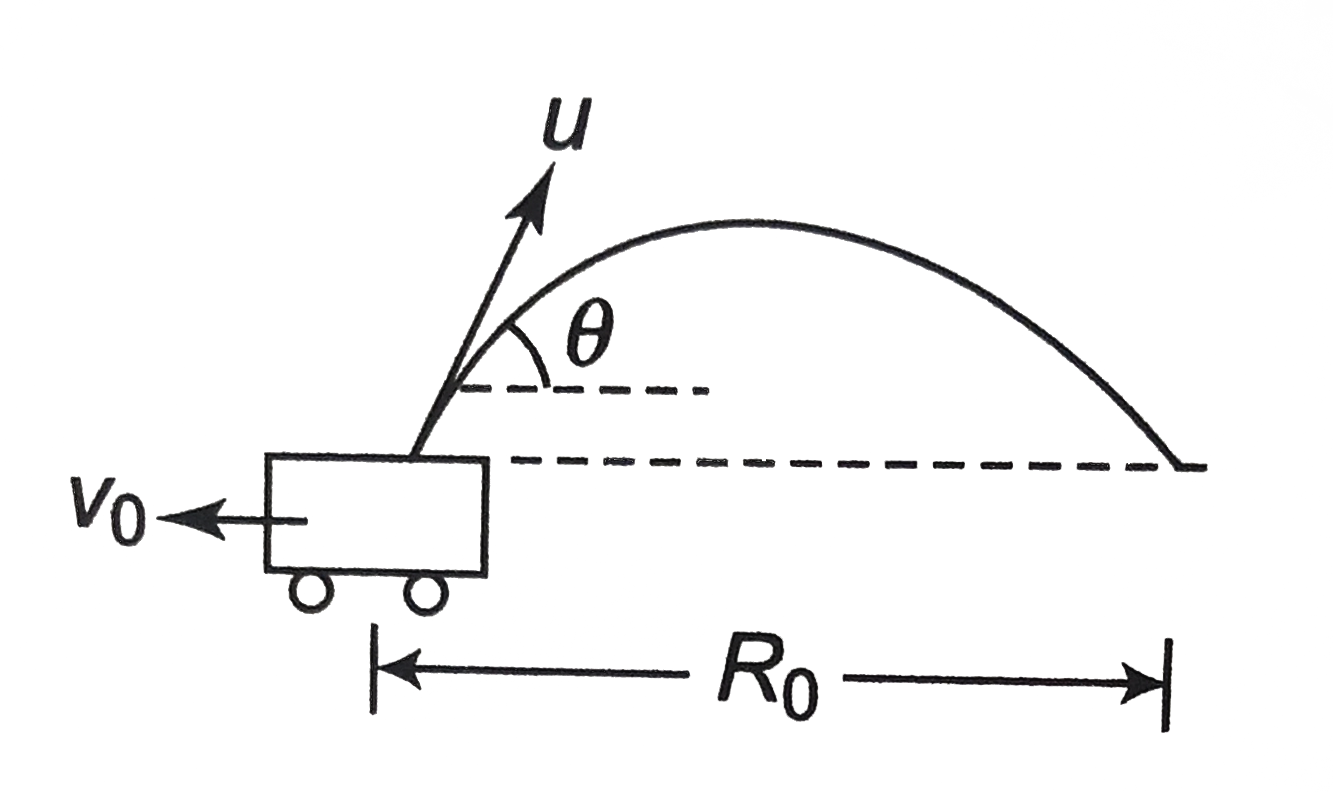
Horizontal component =ucosθ−v0
R0=(ucosθ−v0)T......(iii)
Dividing (ii) by (iii), we get
RR0=ucosθ+v0ucosθ−v0
ucosθ=(R+R0)v0R−R0.........(iv)
R(ucosθ+v0)T
=[(R+R0)v0R−R0+v0]2usinθg
usinθ=g(R−R0)4v0........(v)
Dividing (v) by (iv), we get
tanθ=g(R−R0)24v20(R+R0)
θ=tan−1[g(R−R0)24v20(R+R0)]
Topper's Solved these Questions
Similar Questions
A gun is fired from a moving platform and the ranges of theshot are observed to be R and S when platform is moving forward or backward respectively with velocity v prove that the elevation of the gun is
tan−1[g(R−S)24V2(R+S)]
View SolutionSuppose a person of mass m stands at the edge of a circular platform of radius R and moment of inertia I. The platform is at rest initially, but the platform begins to rotate when the person begins to move with velocity v. Determine the angular velocity of the platform.
View Solution
Knowledge Check
A particle is thrown from a stationary platform with velocity v at an angle of 60∘ with the horizontal. The range obtained is R. If the platform moves horizontally in the direction of target with velocity v, the range will increase to :
A3R2B5R2C2RD3RIf the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
Acos−1(V2Rg)Bcos−1(gRV2)C12(V2Rg)D12sin−1(gRV2)A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity ω0 . When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as
A B
B C
C D
D
A man of mass m1 = 80 kg is standing on a platform of mass m2 = 20 kg that lies on a frictionless horizontal surface. The man starts moving on the platform with a velocity vr = 10 m/s relative to the platform. Find the recoil speed of the platform.
View SolutionFigure-1.52 showns a hemisphere and a supported rod. Hemisphere is moving in right direction with a uniform velocity v2 and the end of rod which is in contact with ground is moving in left direction with a velocity v1. Find the rate at which the angle θ is changing in terms of v1,v2, R and θ.
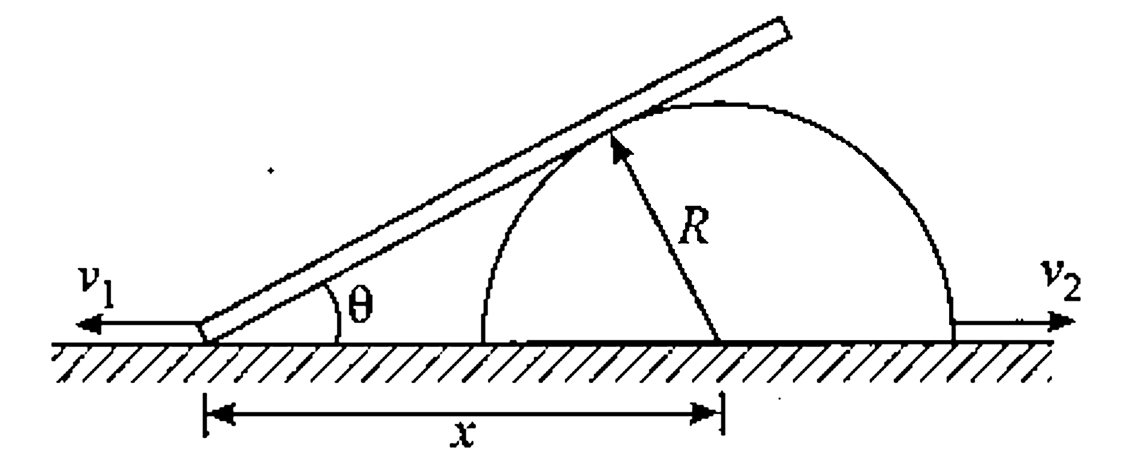
View SolutionA gun of mass M(including the carriage) fires a shot of mass m. The gun along with the carriage is kept on a smooth horizontal surface. The muzzle speed of the bullet vr is constant. Find
(a) The elevation of the gun with horizontal at which maximum range of bullet with respect to the ground is obtained.
(b) The maximum range of the bullet.
View SolutionA man of mass m1 is standing on a platform of mass m2 kept on a smooth horizontal surface. The man starts moving on the platform with a velocity vr relative to the platform. Find the recoil velocity of platform.
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform Now, the platform is given an angular velocity ω0. When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as -
View Solution
