A harmonic wave travelling along the position direction of X-axis is represented by the equation : ξ=0.3×10−4cos(2207t−1.57x), where ξ, t ant x are in cm , second and metre respectively.Deduce the (i)amplitude (ii)wavelength and (iii)time period.
The correct Answer is:(i)0.3×10−4cm(ii)4m(iii)0.2s
Step by step video, text & image solution for A harmonic wave travelling along the position direction of X-axis is represented by the equation : xi=0.3xx10^(-4) cos (220/7t-1.57x), where xi, t ant x are in cm , second and metre respectively.Deduce the (i)amplitude (ii)wavelength and (iii)time period. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A harmonic oscillation is represented by
y=0.34cos(3000t+0.74) where y and t are in mm and second respectively. Deduce
amplitude,
frequency and angular frequency,
time period and
intianl phase.
View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by
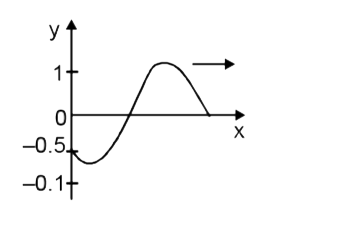
View Solution
Knowledge Check
A wave is represented by the equation, y=0.1sin(60t+2x), where x and y are in metres and t is in seconds. This represents a wave
Atravelling with a speed of 130 m/s, in the negative x directionBtravelling with a speed of 30 m/s, in the positive x directionCof wavelength 30π metreDof frequency (30π) hertzThe equation of a plane progressive wave travelling along positive direction of x−axis is y=rsin[2πtT−2πxλ] where y= displacement of particle at (x,t),r= amplitude of vibratio of particle, T= time period of wave motion, λ= wavelength of wave ,x= starting distance of wave from the origin. Velocity of wave,
υ=vλ=λT= constant.
Acceleration of wave, a=0.
Velocity of particle at time t=dydt
Acceleration of particle at time t=d2ydt2
A harmonic wave travelling along positive direction of x axis is represented by
y=0.25×10−3sin(500t−0.025x)
where x and y are in metre and t is in second
The amplitude of vibration of particle isA0.25×10−3cmB0.25×10−3mC500mD0.025mThe amplitude of a wave represented by the equation y=3sin(5x−0.5t)+4cos(5x−0.5t), is
A7B4C3D5
A tavelling harmonic wave is represented by the equation y(x,t)=10−3 sin (50t+2x), where x and Y are in meter and t is in seconds . Which of the following is a correct statement about the wave?
View SolutionThe equation of a plane progressive wave is give by equation
y=10sin2π(t−0.005x)
where y and x are in cm and t is in seconds. Calculate the amplitude, frequency, wavelength and velocity of the wave.
View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by :-
_E01_059_Q01.png) .
.
View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by
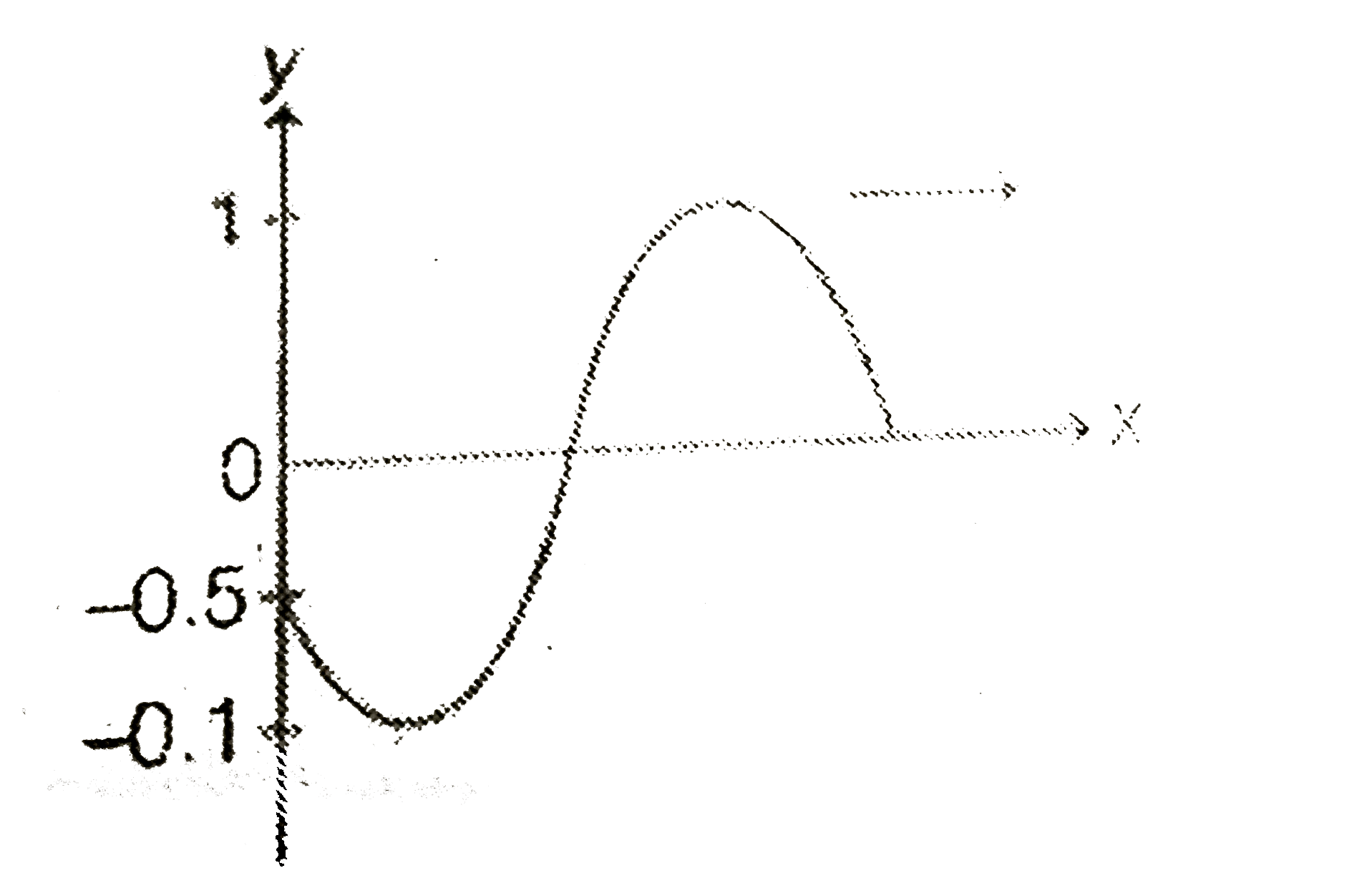
View SolutionA wave equation which gives the displacement along the Y direction is given by the equation y=104sin(60t+2x), where x and y are in metres and t is time in seconds. This represents a wave
View Solution
