A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-

Video Solution

Text Solution

Verified by Experts

Let T = mg at angle $θ$ as shown in figure.
$h = l (1 - cos θ)$ ...(i)
Applying conservation of mechanical energy between points A and B, we get
$\frac{1}{2} m (u^{2} - v^{2}) = m g h$

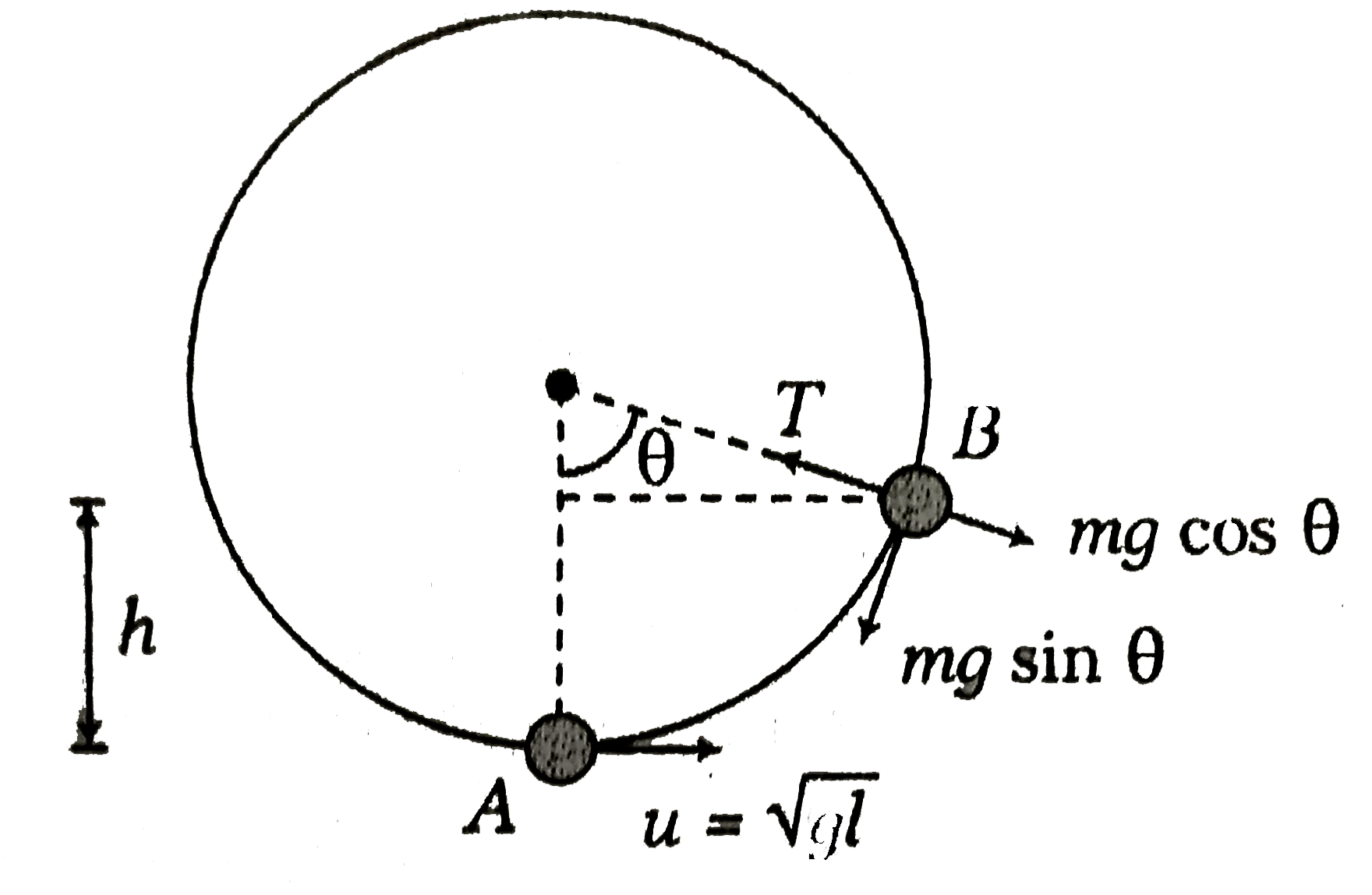
Here, $u^{2} - g l$ ....(ii)
and v= speed o f particle in position B
$∴ u^{2} = u^{2} - 2 g h$ ....(iii)
Further, $T - mg cos θ = \frac{m v^{2}}{l}$
or $m g - mg cos θ = \frac{m v^{2}}{l} (T = m g)$
or $v^{2} = g l (1 - cos θ)$ ...(iv)
substituting values of $v^{2}, u^{2}$ and h from Eqs. (iv), (ii) and (i) in Eq. (iii), we get
$g l (1 - cos θ) = g l - 2 g l (1 - cos θ)$
or $cos θ = \frac{2}{3}$
or $θ = {cos}^{- 1} (\frac{2}{3})$
substituting $cos θ = \frac{2}{3}$ in Eq. (iv), we get
$v = \sqrt{\frac{g l}{3}}$

Updated on:21/07/2023