A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is 1. Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log.
Step by step video & image solution for A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is 1. Determine the period T of small oscillations of the system in a vertical plane perpendicular to the log. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A load of mass M is on horizontal rails. A pendulum made of a ball of mass m tied to a weightless inextensible thread is suspended to the load. The load can move only along the rails. Determine the ratio of the periods T2/T1 of small oscillations of the pendulum in vertical planes parallel and perpendicular to the rails.
View SolutionOne rope of a swing is fixed above the other rope by b. The distance between the poles of the swing is a. The lengths l1 and l2 of the ropes are such that l21+l22=a2+b2 (Fig ).
Determine the period T of small oscillations of the swing, neglecting the height of the swinging person in comparison with the above lengths.

View Solution
Knowledge Check
A thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23mA man is swinging on a swing made of 2 ropes of equal length L and in direction perpendicular to the plane of paper. The time period of the small oscillations about the mean position is
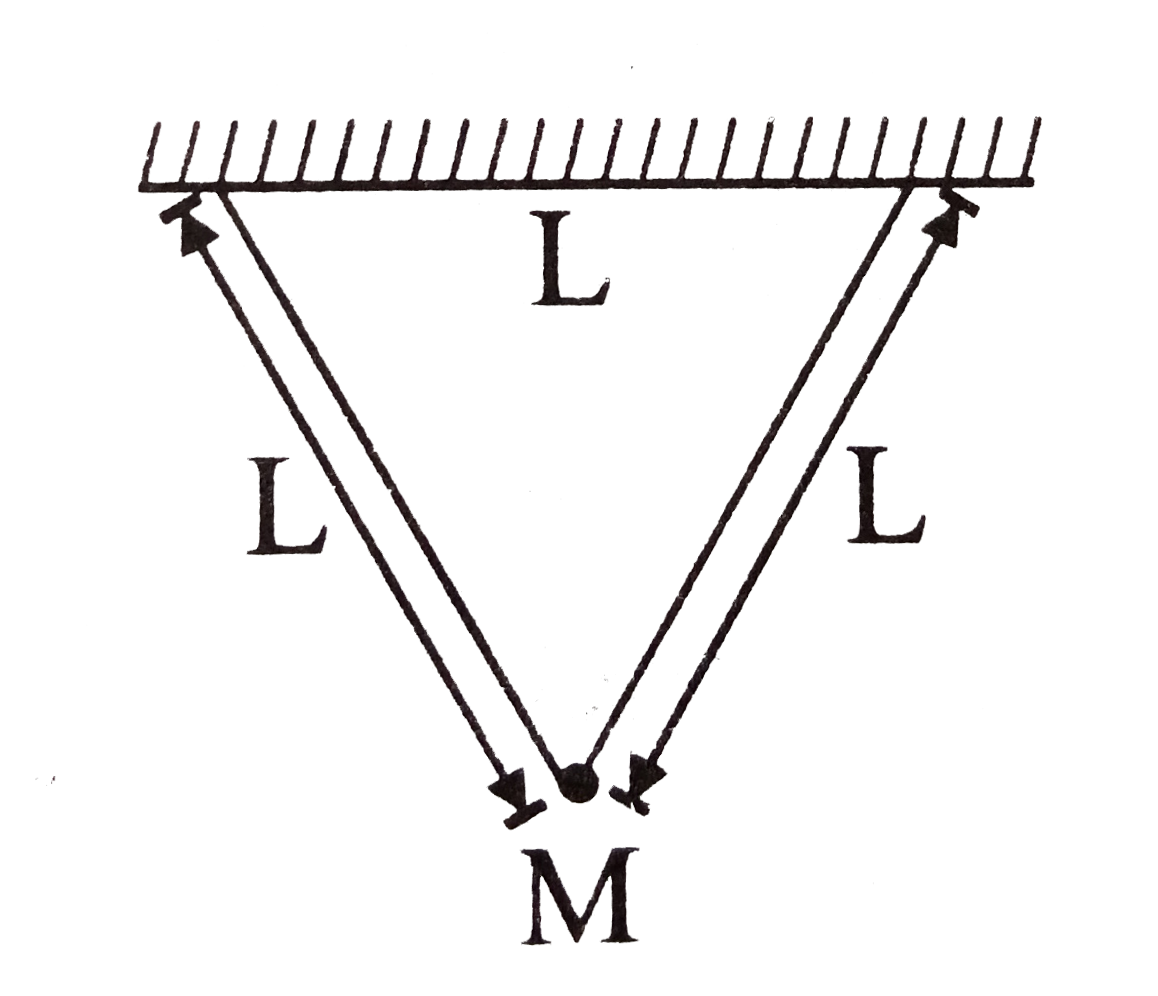 A2π√L2gB2π√√3L2gC2π√L2√3gDπ√Lg
A2π√L2gB2π√√3L2gC2π√L2√3gDπ√LgTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
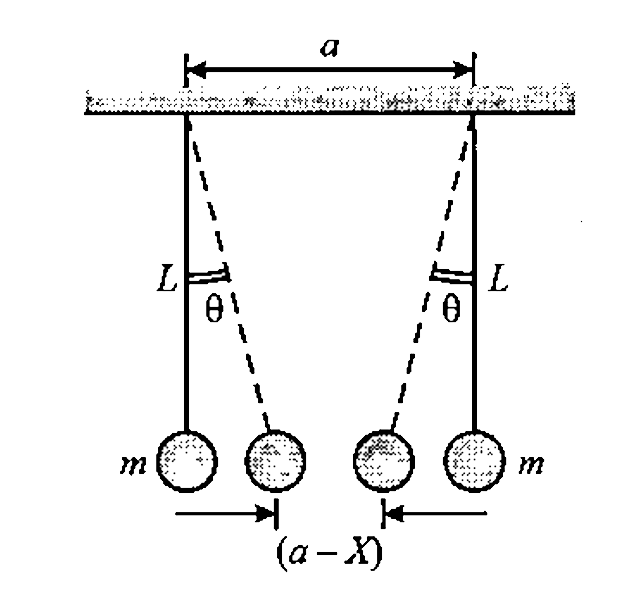 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
A solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
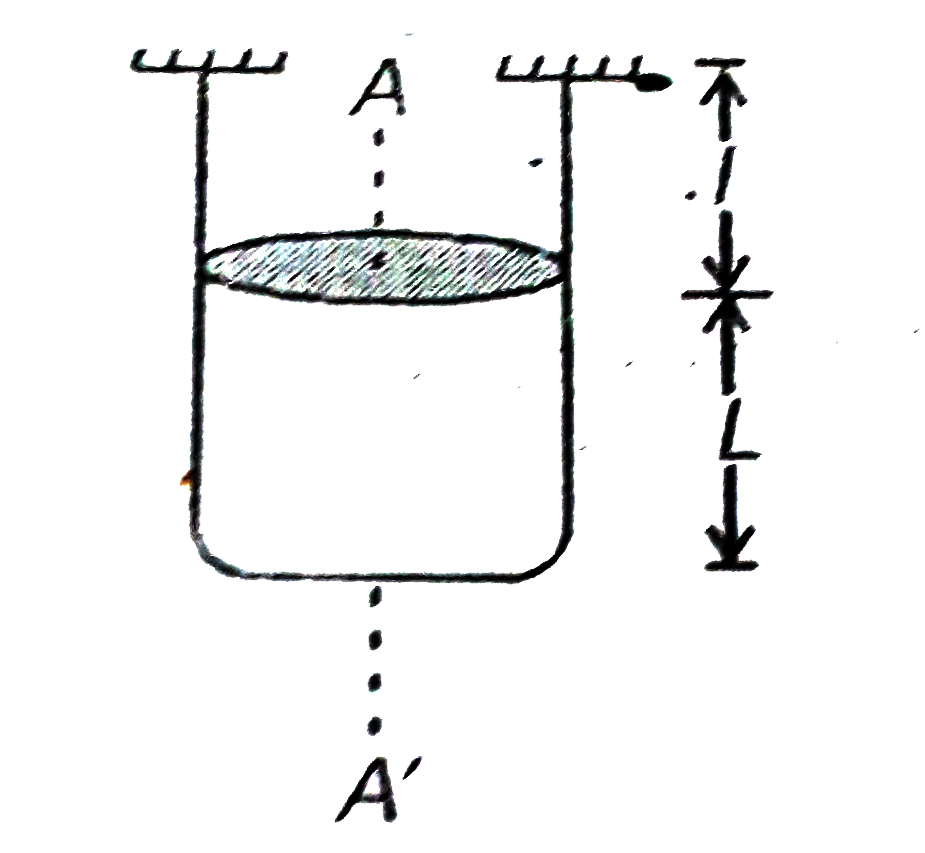
View SolutionA simple pendulum oscillating with a small amplitude has a time period of T=1.0s . A horizontal thin rod is now placed beneath the point of suspension at a distance equal to half the length of the pendulum. The string collides with the rod once in each oscillation and there is no loss of energy in such collisions. Find the new time period T of the pendulum
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
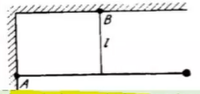
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
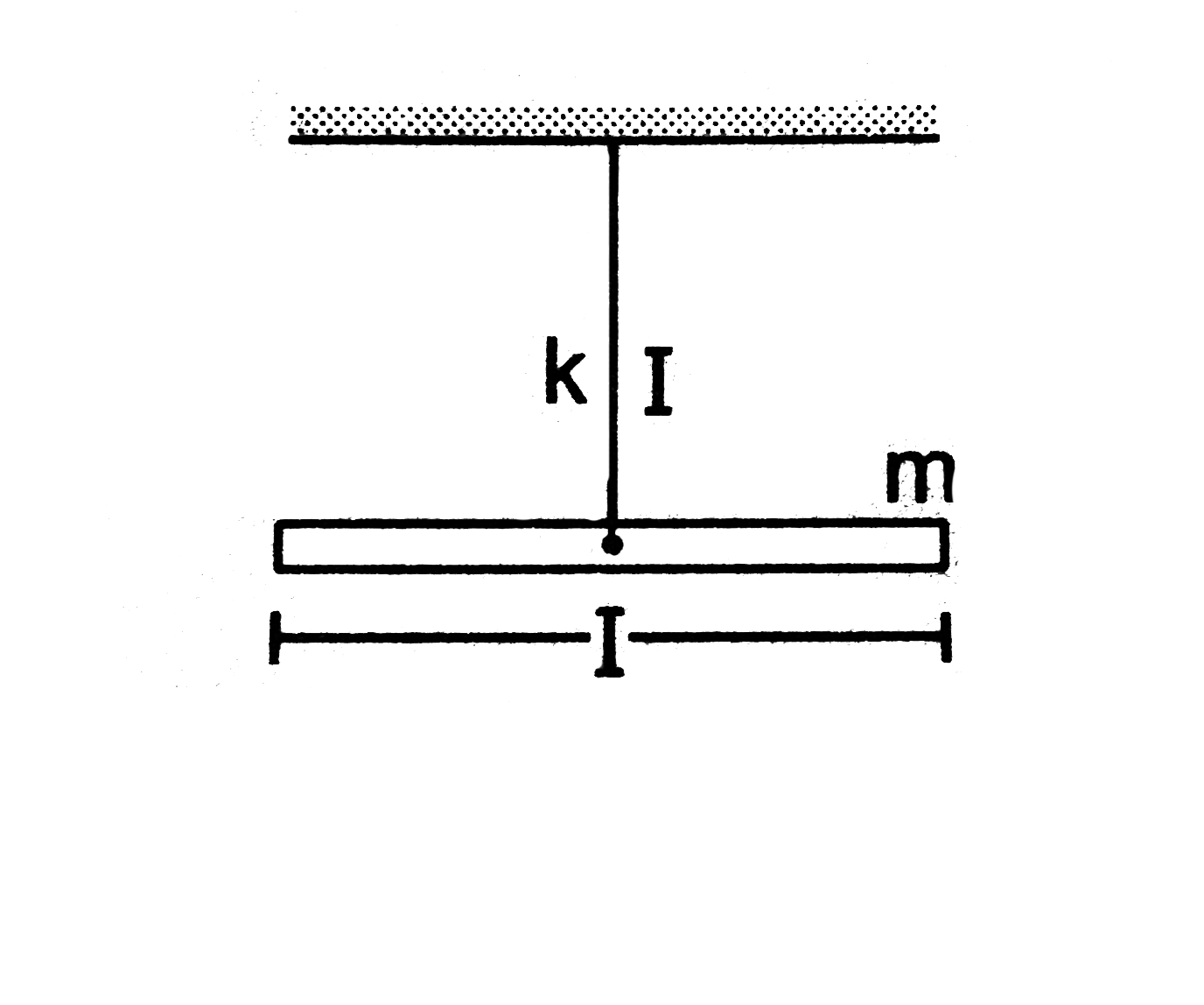
View SolutionA ball of mass m is suspended from a rope of length L. It describes a horizontal circle of radius r with speed v. the rope makes an angle θ with vertical given by sinθ=r/2. Determine (a) the tension in the rope and (b) the speed of the ball. (c) time period of ball.
View Solution
