A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density $ρ$ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

A

$M g$

B

$M g - V ρ g$

C

$M g + π R^{2} h ρ g$

D

$ρ g (V + π R^{2} h)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

According to Archimedes' principle upthrust weight of the fluid displaced $F_{bottom} - F_{top} = V ρ g$

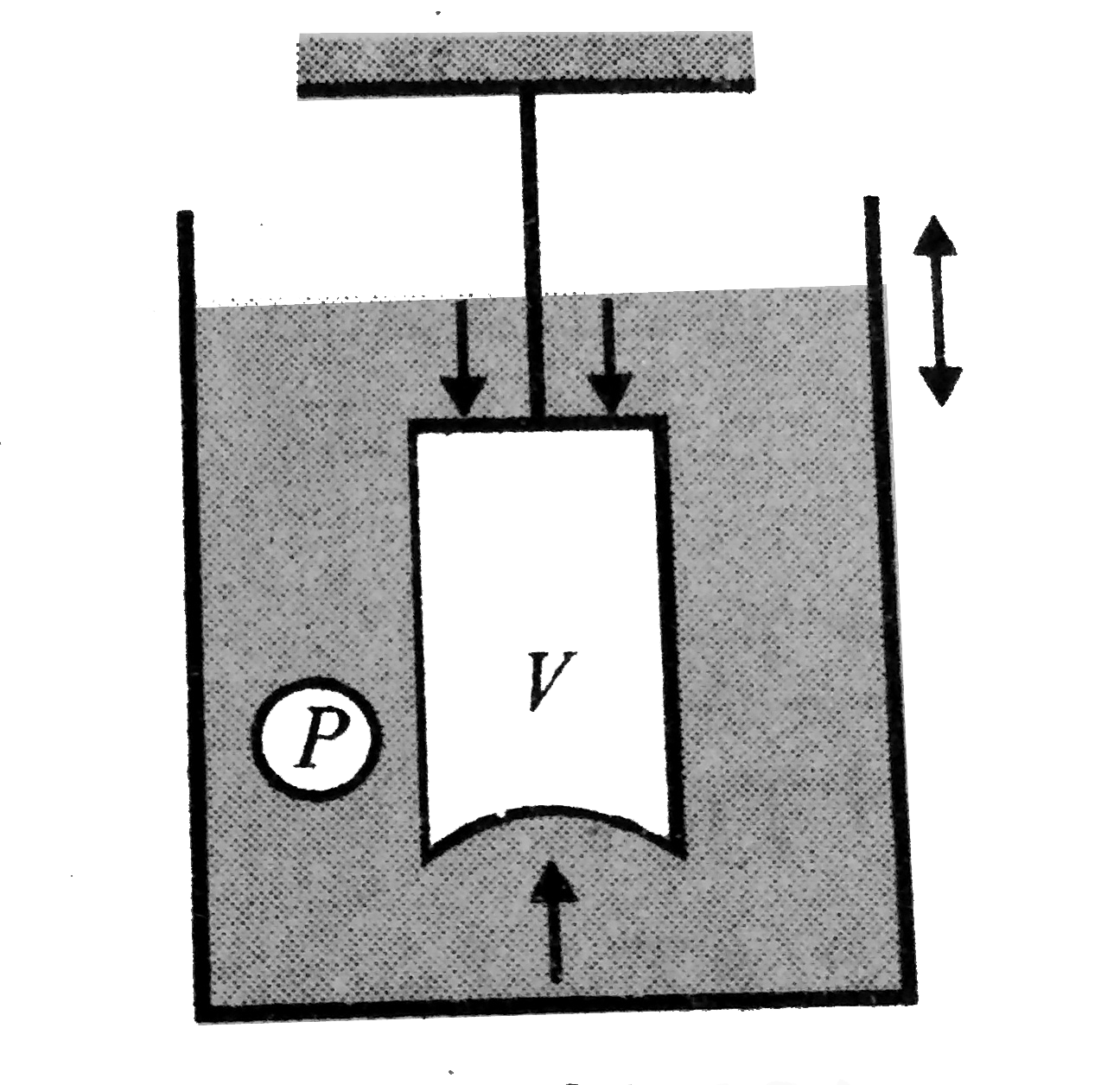
$∴ F_{bottom} = F_{top} + V ρ g$
$= P_{1} \times A + V ρ g$
$= (h ρ g) \times (π R^{2}) + V ρ g$
$= ρ g [π R^{2} h + V]$

|

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density $ρ$ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is

AMg
BMg - h $ρ$ g
C $M g + π R^{2} h ρ g$
D $ρ g (V + π R^{2} h)$
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density $ρ$ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

AMg
BMg-Vdg
C $M g + π R^{2} h d g$
D $d g (V + π R^{2} h)$
A conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density $ρ$ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

AMg
B $M g - V ρ g$
C $M g + π R^{2} h ρ g$
D $ρ g (V + π R^{2} h)$

CENGAGE PHYSICS-FLUID MECHANICS-SCQ_TYPE

Home
Ask Doubt
Profile