A hollow sphere of external radius R and thickness t(<<R) is made of a metal of density ρ. The sphere will float in water if (Take density of water = 1 g cm−3 )
t≤Rρ
t≤R3ρ
t≤R2ρ
t≥R3ρ
The correct Answer is:B
To determine the condition for a hollow sphere to float in water, we start by analyzing the forces acting on the sphere.
1. Understanding the Problem: We have a hollow sphere with an external radius R and thickness t (where t≪R). The density of the metal used to make the sphere is ρ, and the density of water is 1g/cm3.
2. Floating Condition: For the sphere to float, the buoyant force acting on it must be equal to or greater than its weight. The buoyant force is equal to the weight of the water displaced by the submerged part of the sphere.
3. Calculating the Volume of the Sphere:
- The volume V of the hollow sphere can be calculated as the difference between the volume of the outer sphere and the inner sphere.
- The volume of the outer sphere is given by:
Vouter=43πR3
- The inner radius Rinner is R−t. Thus, the volume of the inner sphere is:
Vinner=43π(R−t)3
- Therefore, the volume of the hollow part of the sphere is:
V=Vouter−Vinner=43πR3−43π(R−t)3
4. Simplifying the Volume:
- We can simplify the expression for the volume of the hollow sphere:
V=43π(R3−(R−t)3)
- Using the binomial expansion for (R−t)3:
(R−t)3=R3−3R2t+3Rt2−t3
- Thus, we have:
V = \frac{4}{3} \pi \left( 3R^2t - 3Rt^2 + t^3 \right) \approx \frac{4}{3} \pi (3R^2t) \quad \text{(since t \ll R )}
- Therefore:
V≈4πR2t
5. Weight of the Sphere:
- The weight W of the sphere can be calculated using its volume and density:
W=V⋅ρ=4πR2t⋅ρ
6. Buoyant Force:
- The buoyant force Fb is equal to the weight of the water displaced:
Fb=Volume of water displaced⋅Density of water=V⋅1g/cm3=4πR2t⋅1
7. Setting Up the Equation:
- For the sphere to float:
Fb≥W
- Therefore:
4πR2t≥4πR2t⋅ρ
8. Solving for Thickness t:
- Dividing both sides by 4πR2 (assuming R≠0):
t≥t⋅ρ
- Rearranging gives:
t⋅(1−ρ)≥0
- Since ρ (density of the metal) must be less than or equal to the density of water for the sphere to float:
ρ≤1g/cm3
Final Condition:
The thickness t must satisfy:
t≤R3⋅(1−ρ)
- The volume V of the hollow sphere can be calculated as the difference between the volume of the outer sphere and the inner sphere.
- The volume of the outer sphere is given by:
Vouter=43πR3
- The inner radius Rinner is R−t. Thus, the volume of the inner sphere is:
Vinner=43π(R−t)3
- Therefore, the volume of the hollow part of the sphere is:
V=Vouter−Vinner=43πR3−43π(R−t)3
- We can simplify the expression for the volume of the hollow sphere:
V=43π(R3−(R−t)3)
- Using the binomial expansion for (R−t)3:
(R−t)3=R3−3R2t+3Rt2−t3
- Thus, we have:
V = \frac{4}{3} \pi \left( 3R^2t - 3Rt^2 + t^3 \right) \approx \frac{4}{3} \pi (3R^2t) \quad \text{(since t \ll R )}
- Therefore:
V≈4πR2t
- The weight W of the sphere can be calculated using its volume and density:
W=V⋅ρ=4πR2t⋅ρ
- The buoyant force Fb is equal to the weight of the water displaced:
Fb=Volume of water displaced⋅Density of water=V⋅1g/cm3=4πR2t⋅1
- For the sphere to float:
Fb≥W
- Therefore:
4πR2t≥4πR2t⋅ρ
- Dividing both sides by 4πR2 (assuming R≠0):
t≥t⋅ρ
- Rearranging gives:
t⋅(1−ρ)≥0
- Since ρ (density of the metal) must be less than or equal to the density of water for the sphere to float:
ρ≤1g/cm3
The thickness t must satisfy:
t≤R3⋅(1−ρ)
Topper's Solved these Questions
- NSO QUESTION PAPER 2019 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2019 SET AEXERCISE - ACHIEVERS SECTION
2 Videos
- NSO QUESTION PAPER 2018 SET B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2018 SET B EXERCISE - ACHIEVERS SECTION
4 Videos
- NSO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2019 SET BEXERCISE - ACHIEVERS SECTION
1 Videos
Similar Questions
A hollow metal sphere of external radius 2cm, thickness t, just sinks in water. Find the value of t in centimetre. Given specififc gravity of metal is 2.5.
View SolutionA solid sphere of radius R has a concentric cavity of radius R3 inside it. The sphere is found to just float in water with the highest point of it touching the water surface. Find the specific gravity of the material of the sphere.
View Solution
Knowledge Check
A hollow sphere of external radius R and thickness t (< < R) is made of a metal of density ρ. The sphere will float in water if
At≤RρBt≤R3ρCt≤R2ρDt≥R3ρA hollow sphere of mass M and radius r is immersed in a tank of water (denstiy ρw). The sphere would float if it were set free. The sphere is tied to the bottom of the tank by two wires which makes angle 45∘ with the horizontal as shown in the figure. The tension T1 in the wire is :
 A43πR3ρwg−Mg√2B23πR3ρwg−MgC43πR3ρwg−Mg2D43πR3ρwg+Mg
A43πR3ρwg−Mg√2B23πR3ρwg−MgC43πR3ρwg−Mg2D43πR3ρwg+MgThe radius of the biggest metal coin of thickness t and density ρ which would be able to float on water surface of surface of water is ρ
AS2ρgtBSρgtC2SρgtD4S3ρgt
A hollow sphere of external and internal diameter 4 cm and 2 cm, respectively, floats in a liquid of density 3.5 g cm−3. The level of the liquid coincides with the center of the sphere. Calculate the density of the material of the sphere.
View SolutionA hollow sphere of radius R is filled completely with an ideal liquid of density ρ .Sphere is moving horizontally with an acceleration 2g ,where g is acceleration due to gravity in the space.If minimum pressure of liquid is P0 ,then pressure at the centre of sphere is
View SolutionA solid sphere of radius R has a concentric cavity of radius 'R/2' inside it. The sphere is found to just float in water with the highest point of it touching the water surface. The specific gravity of the material of the sphere is
View SolutionA hollow sphere of simple pendulum is first filled with mercury and then with water. The time periods are in the ratio of their densities are in the ratio 13.6:1
View SolutionOn heating water, bubbles beings formed at the bottom of the vessel detatch and rise. Take the bubbles to be spheres of radius R and amking a circular contact of radius r with the bottom of the vessel. If r<<R, and the surface tension of water is T, value of r just before bubles detatch is : (density of water is ρw)
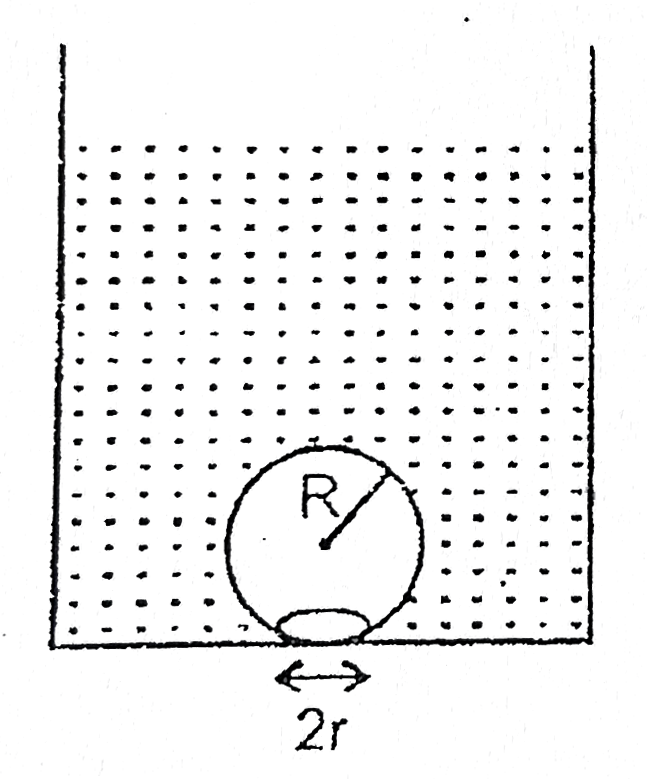
View Solution
