A horizontal cylinder closed from one end is rotated with a constant angular velocity ω about a vertical axis passing through the open end of the cylinder. The outside air pressure is equal to p0, the temperature to T, and the molar mass of air to M. find the air pressure as a function of the distance r from the rotate axis. The molar mass is assumed to be independent of r.
Let us consider the mass element of the gas (thin layer) in the cylinder at a distance r from its open end as shown in the figure.
Using Newton's second law for the element
Fn=mwn :
(p+dp)S−pS=(ρSdr)ω2r
or, dp=ρω2rdr=pMRTω2rdr So, dpp=Mω2RTrdr or, ∫pp0dpp=Mω2RT∫r0rdr,
Thus, 1npp0=Mω22RTr2 or, p=p0eMω2r2/RT.
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The First Law Of Thermodynamics - Heat Capacity
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A horizontal tube with closed ends is rotated with a constant angular velocity ω about a vertical axis passing through one of its ends. The tube contains carbon dioxide at a temperature T=300K. The length of the tube is l=100cm. Find the value ω at which the ratio of molecular concentrations at the opposite ends of the tube is equal to η=2.0.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution
Knowledge Check
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]a semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is
 A(a) BωR2/2B(b) 2BωR2C( c) is variableD(d) none of these
A(a) BωR2/2B(b) 2BωR2C( c) is variableD(d) none of these
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
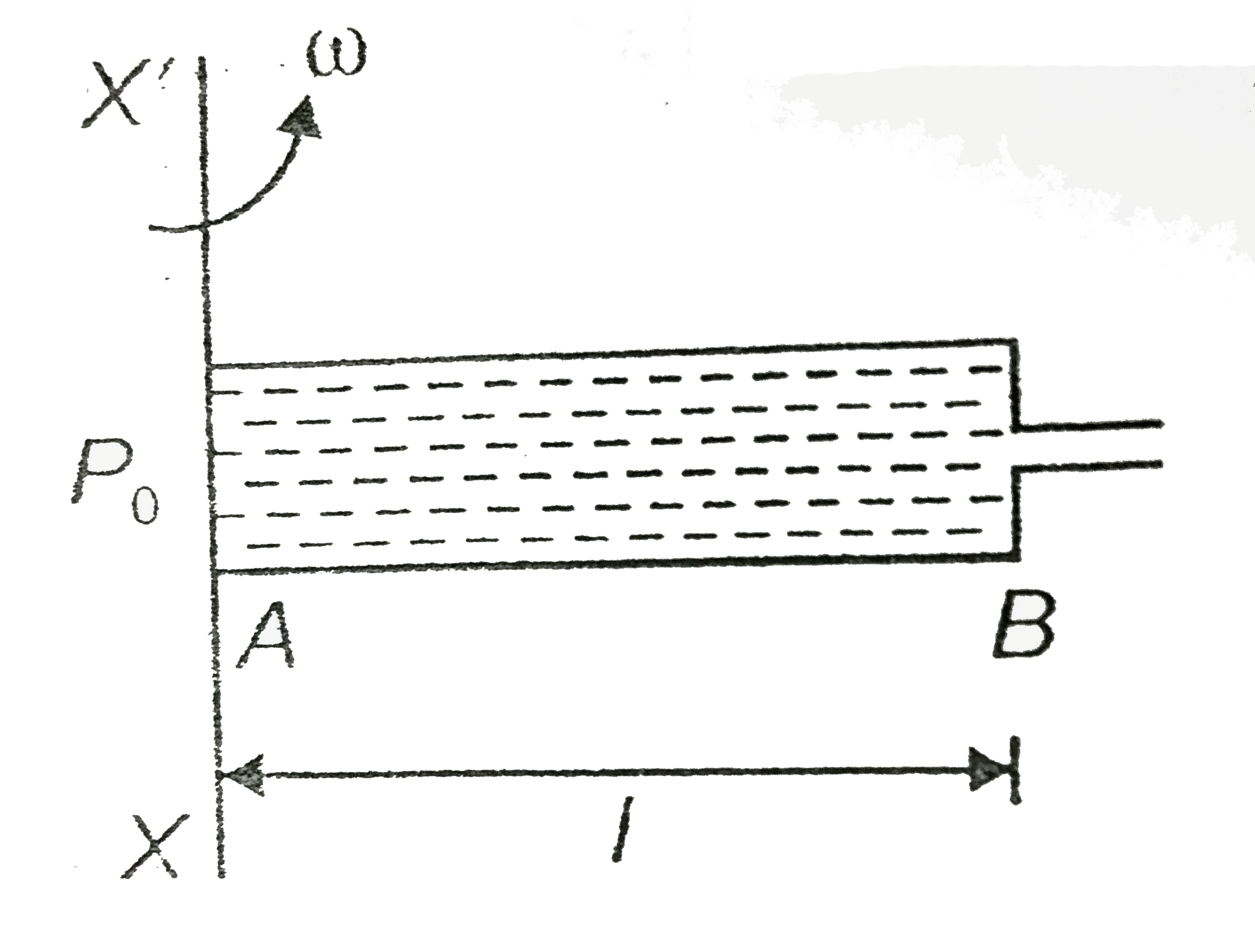
View SolutionA horizontally orientd tube of length l rotates with a constant angular velocity ω about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid.
The end A of tube is having pressure P0. The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0
View SolutionAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
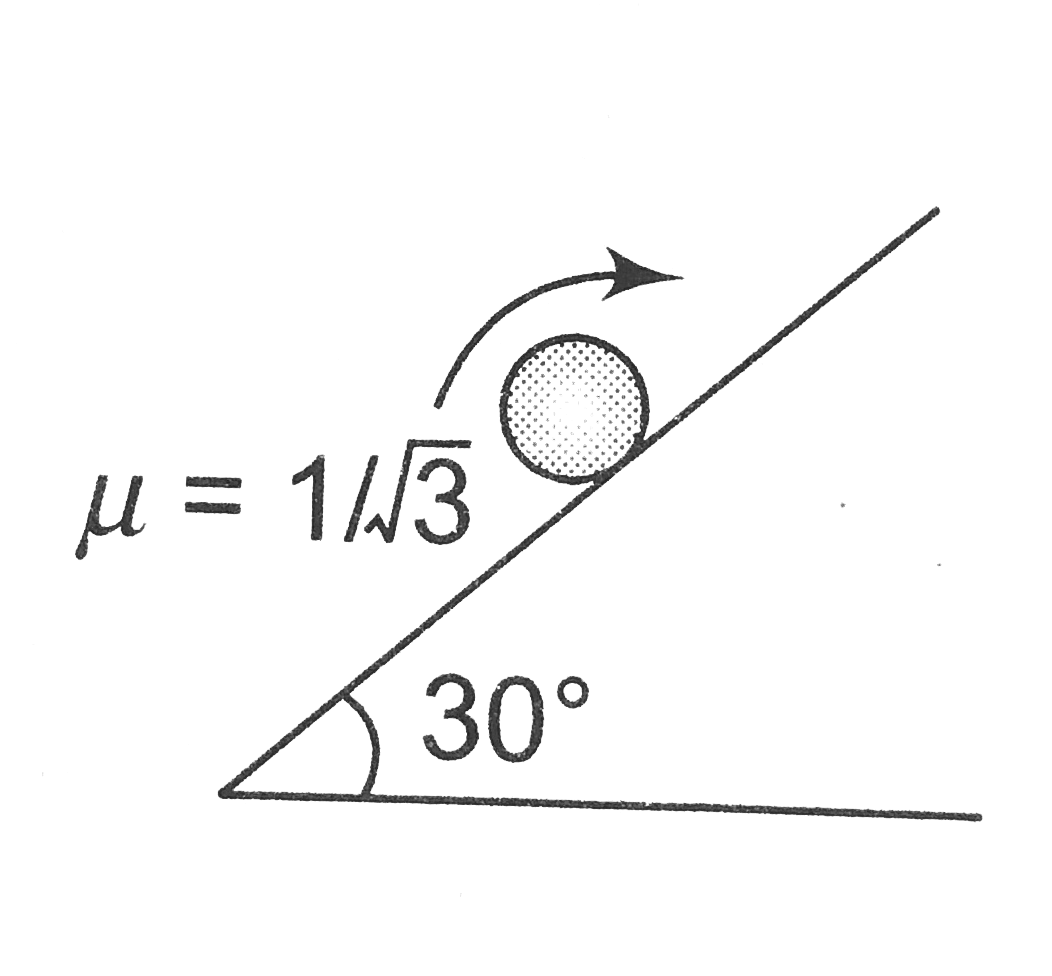 .
.
View Solution
