A horizontal force F is applied to a homogeneous rectangular block of mass m, width b and height H. The block moves with constant velocity, the coefficient of friction is μk.
a. What is the greater height h at which the force F can be applied so that the block will slide without tipping over ?
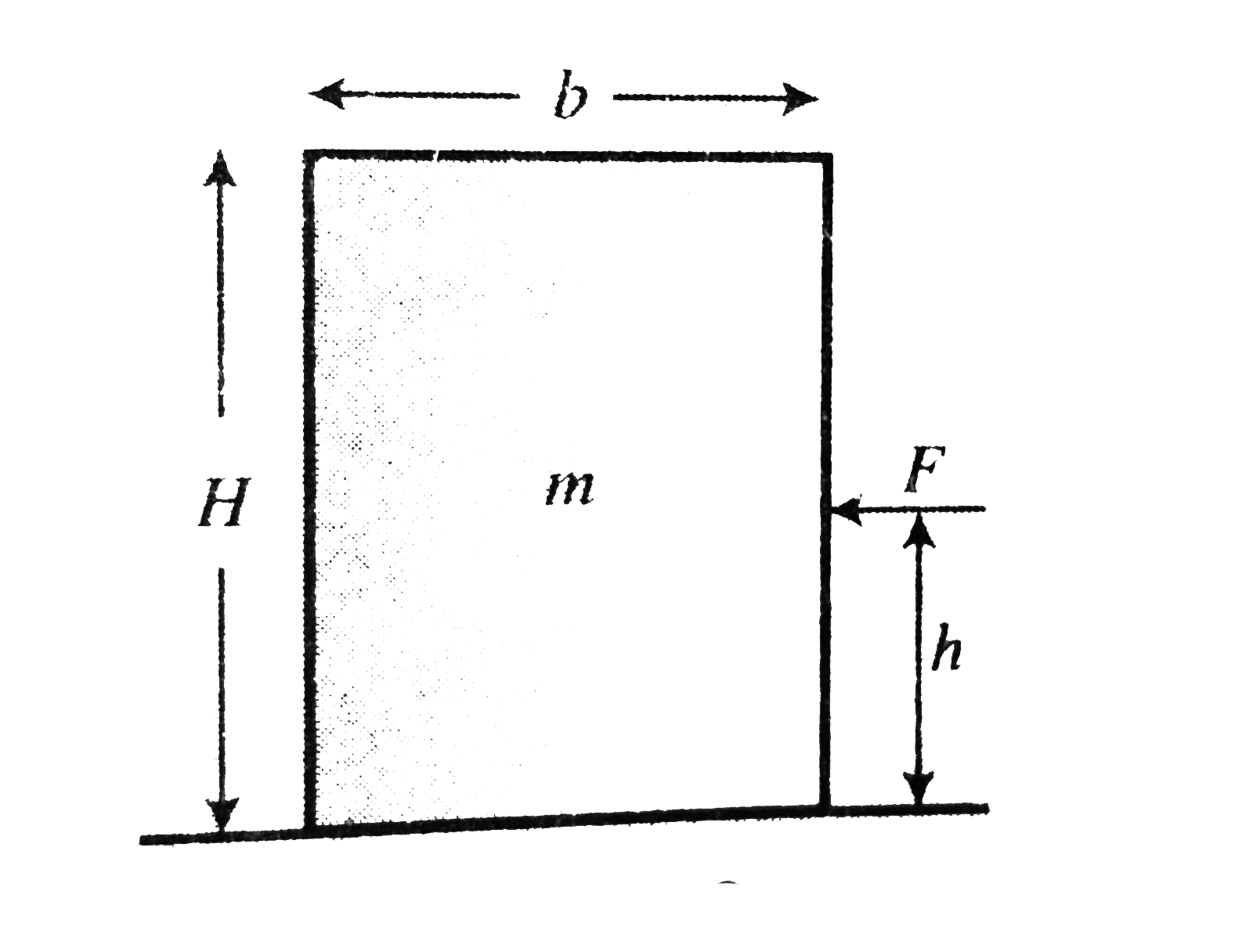
b. Through which point on the bottom face of the block will the resultant of the friction and normal forces act if h=H/2?
c. If the block is at rest and coefficient of static friction is μs what are the various criteria for which sliding or tipping occurs?
a. In the absence of any external force in horizontal direction the normal reaction N passes through the centre of mass of the block, when force F is applied, normal reaction shifts in the direction of applied force F.
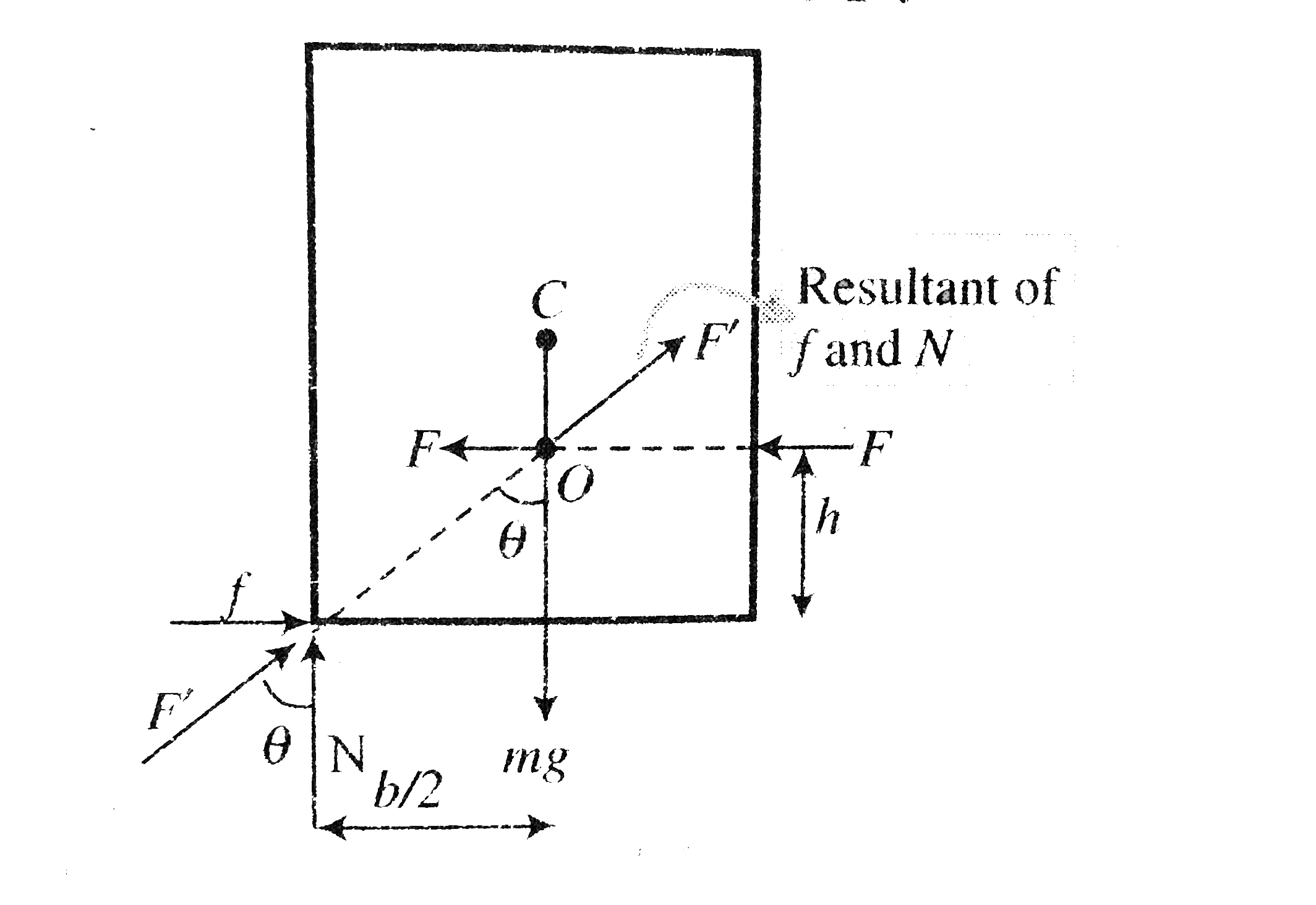
Since right part of body is having tendency to lift from surface, at the instant of tipping over about the edge the normal reaction passes through edge. from the conditionns of equilibrium.
In horizontal directionn f=F=μkmg
In vertical direction N=mg
Balancing torque about edge Fh−mgb2
or h=mgb2F=mgb2μkmg=b2μk
We can solve the problems by another approach also as the resultant of friction force (μkN) and the normal reactiong must pass through the same point through which F passes, since three coplanar forces keeping a body inequilibrium pass through a common point i.e. they should be concurrent.
From Lami's theorem.
F'sin90∘=Fsin(180∘+θ)=mgsin(90∘+θ)
⇒Fsinθ=mgcosθ or tanθ=Fmg=μkmgmg=μk
From figure it is clear tanθ=μkNN=b2h
or b2h=μk⇒h=b2μk
b. In this case we cannot take normal reaction at the edge.

Let normal reaction acts at a distance x from the line of action of mg.
Torque of all the forces about C must be zero.
(μkN×H2)=Nx
x=μkH2
Alternately we can proceed as in part a. Resultant of μkN,N passes through C the interaction of F and mg.
Therefore from geometry of the figure.
xH2=tanθ=μk,x=μkH2
c. As the point of application of force is raised higher, the location of the line of action of the normal reaction N moves to the let. In the limiting case (when the block is about to tip over ), x=b/2. the normal reaction passes through edge as shown in figure.
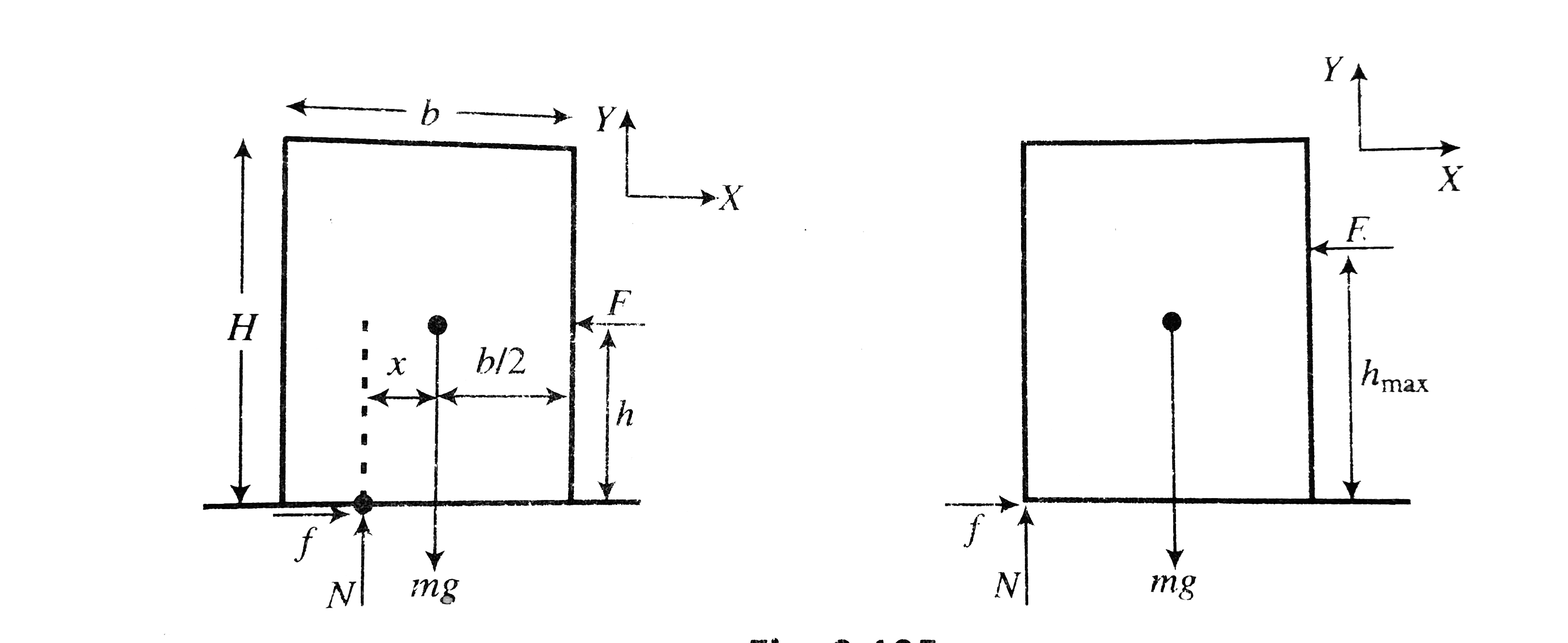
Initial toppling torque about edge:
Fhmax=mgb2 or hmax=mgb2F........i
For initial sliding in horizontal direction F=μN In vertical direction N=mg
Hence, F=μmg......ii
If sliding and tipping are equally likely to occur, we can elimiate F from eqn i and ii to get hmax=b2μ
which is independent of weight mg height H of the body and applied force F.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A block of mass m rests on a horizontal floor for which coefficient of friction is μ . Find the magnitude and the direction of force that should be applied to just move the block so that the applied force is minimum.
View SolutionA tall block of mass M=50kg and base width b=1m and height h=3m is kept on rough inclined surface with coefficient of friction μ=0.8 as shown in figure. The angle of inclination with the horizontal is 37∘. Determine whether the block slides down or topples over.
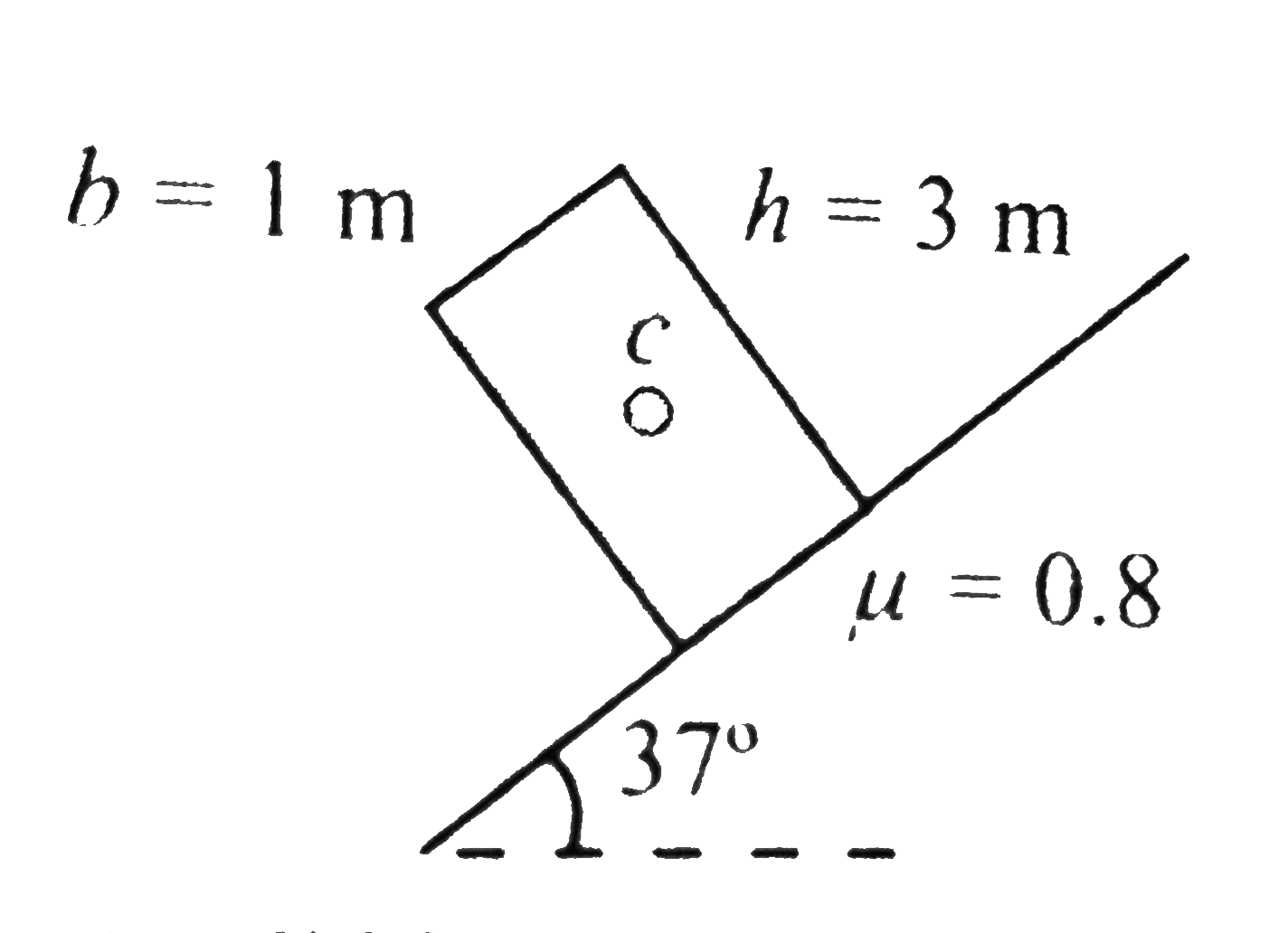
View Solution
Knowledge Check
in the above questions ,F is applied at h/2 The disance x is the horizontal disance between a point on the bottom face of the block at which resultant of friction and normal force act C.G of the block find x-
Aμh2Bμh6Cμh4Dμh3A homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
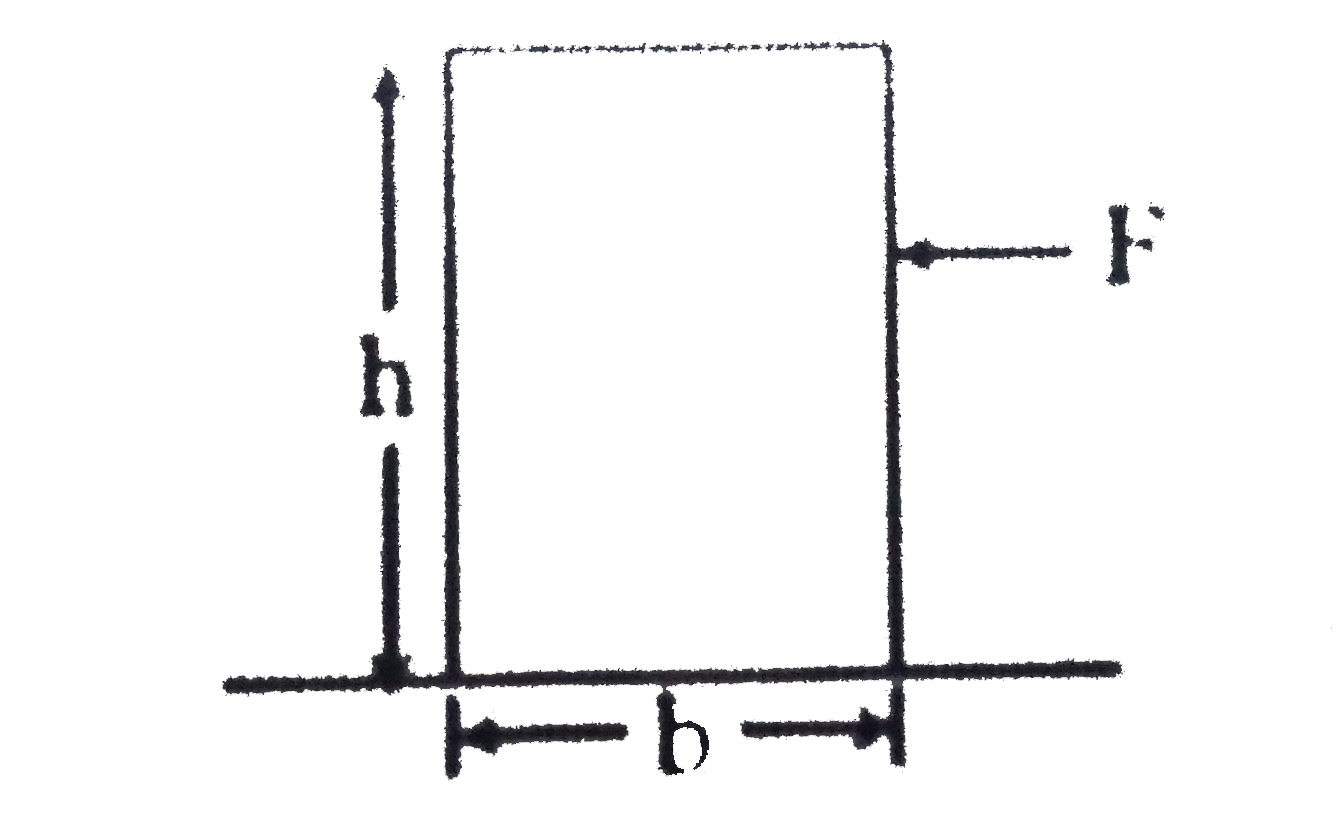 Ab2μB2bμCbμD2√2bμ
Ab2μB2bμCbμD2√2bμA horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be
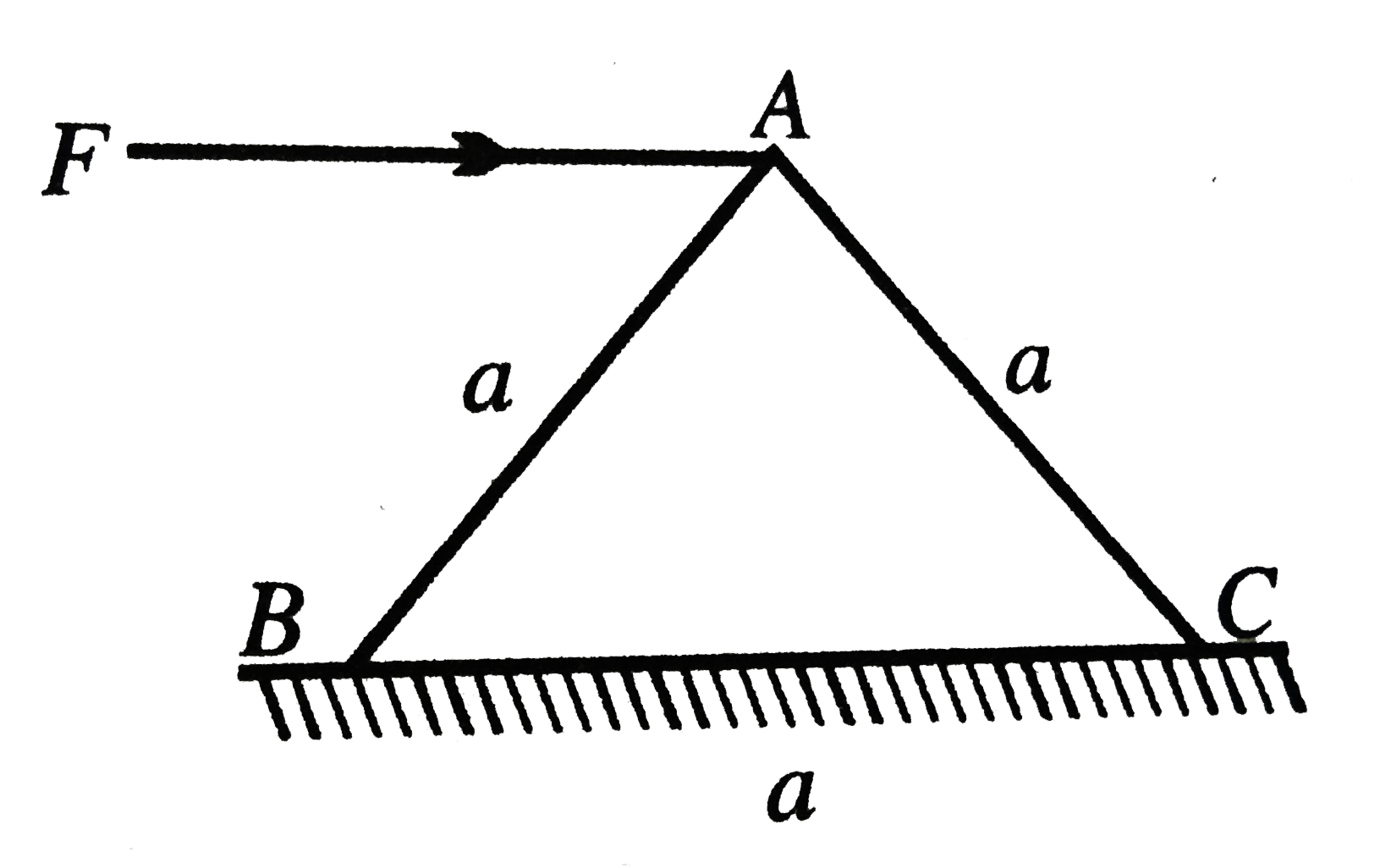 A2√3B13C1√3D12
A2√3B13C1√3D12
Consider the situation shown in the figure . The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied so that two blocks move together.

View SolutionDetermine the maximum ratio h/b for which the homogenous block will side without tipping under the actionof force P. The coefficient of static friction between the block and the incline is μs.

View SolutionA block of mass m rests on a bracket of mass M. The coefficients of friction between block and bracket are μs and μk . The bracket rests on a frictionless surface. What is the maximum force F that can be applied if the block is not to slide on the bracket?
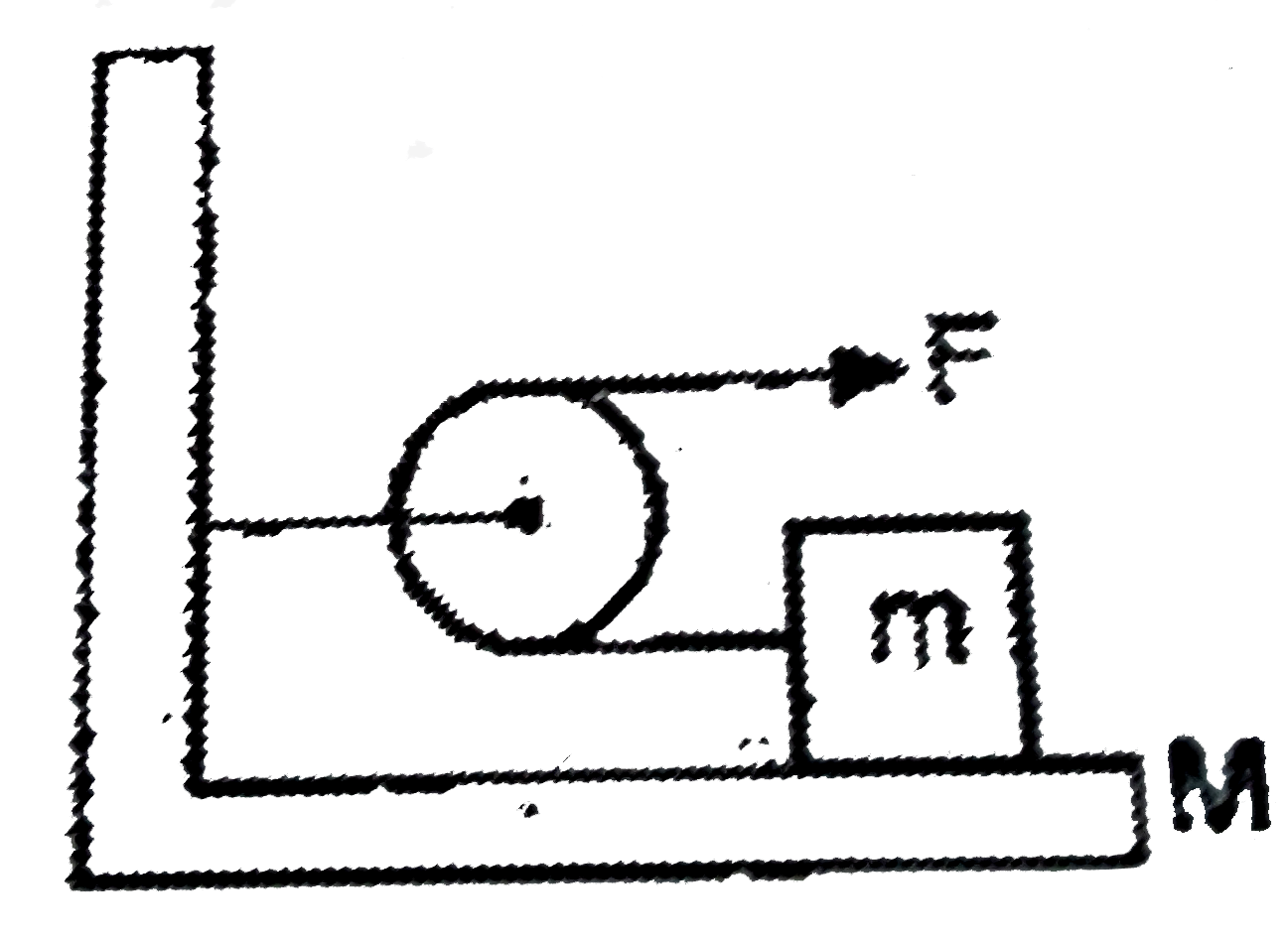
View Solution
In given diagram what is the minimum value of a horizontal external force F on block A so that block B will slide on ground is .
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
View Solution
