A ladder of mass 30 kg and length 5 m is kept leaning against a vertical smooth wall. A man of mass 60 kg climbed up the length of the ladder. If the coefficient of friction between the floor and the ladder is 0.5, what should be the maximum distance of the foot of the ladder from the wall to avoid slipping?
The correct Answer is:3 m
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - Problem Set -II ( Miscellaneous )1videos
STATICS
- BOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - Hots Numerical Problems ( Based on Centre of Mass)2videos
STATICS
- BOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - Problem Set -II (Based on Equilibrium of Force )1videos
STATICS
- BOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER16videos
SIMPLE HARMONIC MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner14videos
SUPERPOSITION OF WAVES
Similar Questions
A ladder leaning against a wall makes an angle of 60o with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.
View SolutionA ladder of length 50 m rests against a vertical wall, at a height of 30 m from the ground. Find the inclination of the ladder with the horizontal. Also find the distance between the foot of the ladder and the wall.
View Solution
Knowledge Check
- Question 1 - Select One or More
In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than
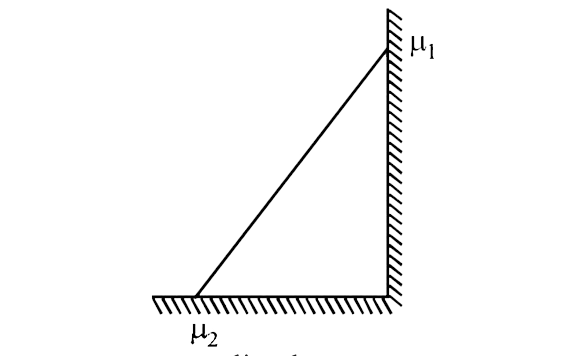 Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
A ladder 10m long is leaning against a vertical wall, it makes an angle of 60° with the ground.How far is the foot of the ladder from the wall?
View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle θ with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View SolutionA ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
View SolutionA ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than
 View Solution
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View Solution

