A large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum length of the rope required to scoop out a bucket full of water through the hole is (0.2x)m. Find the value of x. Take density of ice =0.9 g/cm3
The correct Answer is:5
To solve the problem, we need to analyze the situation of the block of ice floating in water and determine the minimum length of rope required to scoop out a bucket of water through the hole in the ice.
1. Understand the Setup:
- We have a block of ice that is 10 cm thick, floating on a lake.
- There is a vertical hole drilled through the ice.
- The density of ice is given as 0.9g/cm3.
- We need to find the minimum length of rope required to scoop out a bucket of water through the hole, which is given as 0.2x meters.
2. Establish the Forces:
- The block of ice is floating, which means the weight of the ice is balanced by the buoyant force acting on it.
- Let A be the cross-sectional area of the ice block, and y be the depth of the water above the hole.
3. Apply the Principle of Buoyancy:
- The weight of the ice block can be expressed as:
Weight of ice=Vice⋅ρice⋅g=A⋅10cm⋅0.9g/cm3⋅g
- The buoyant force can be expressed as:
Buoyant force=Vdisplaced⋅ρwater⋅g=A⋅(10−y)⋅1g/cm3⋅g
- Setting the weight of the ice equal to the buoyant force gives:
A⋅10⋅0.9⋅g=A⋅(10−y)⋅1⋅g
4. Canceling Common Terms:
- Since A and g are common in both sides, we can cancel them out:
10⋅0.9=10−y
5. Solving for y:
- Rearranging the equation gives:
9=10−y⟹y=10−9=1cm
6. Relating y to the Length of the Rope:
- The minimum length of the rope required to scoop out the bucket of water through the hole is given as 0.2x meters.
- Since y is the depth of the water above the hole, we can equate:
0.2x=1cm
- Converting 1cm to meters gives 0.01m:
0.2x=0.01
7. Solving for x:
- Dividing both sides by 0.2:
x=0.010.2=0.05m
- Converting 0.05m to centimeters gives 5cm.
Final Answer:
The value of x is 5.
- We have a block of ice that is 10 cm thick, floating on a lake.
- There is a vertical hole drilled through the ice.
- The density of ice is given as 0.9g/cm3.
- We need to find the minimum length of rope required to scoop out a bucket of water through the hole, which is given as 0.2x meters.
- The block of ice is floating, which means the weight of the ice is balanced by the buoyant force acting on it.
- Let A be the cross-sectional area of the ice block, and y be the depth of the water above the hole.
- The weight of the ice block can be expressed as:
Weight of ice=Vice⋅ρice⋅g=A⋅10cm⋅0.9g/cm3⋅g
- The buoyant force can be expressed as:
Buoyant force=Vdisplaced⋅ρwater⋅g=A⋅(10−y)⋅1g/cm3⋅g
- Setting the weight of the ice equal to the buoyant force gives:
A⋅10⋅0.9⋅g=A⋅(10−y)⋅1⋅g
- Since A and g are common in both sides, we can cancel them out:
10⋅0.9=10−y
- Rearranging the equation gives:
9=10−y⟹y=10−9=1cm
- The minimum length of the rope required to scoop out the bucket of water through the hole is given as 0.2x meters.
- Since y is the depth of the water above the hole, we can equate:
0.2x=1cm
- Converting 1cm to meters gives 0.01m:
0.2x=0.01
- Dividing both sides by 0.2:
x=0.010.2=0.05m
- Converting 0.05m to centimeters gives 5cm.
The value of x is 5.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Matrix Matching12videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
Similar Questions
A large block of ice 5m thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice =0.9.
 View Solution
View SolutionA large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum of water through the hole is (density of ice =0.9gcm−3)
View SolutionA cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take π2=10 and g=10m/s2)
View SolutionA cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take π2=10 and g=10m/s2)
View SolutionIn the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.
 View Solution
View SolutionThe block is always at rest, the maximum force which can be applied for this is 24x. Find the value of x. Take g = 10 m/s2{coefficient of friction = 0.3}
 View Solution
View SolutionIceberg floats in water with part of it submerged. What is the fraction of the volume of iceberg submerged if the density of ice is ρi=0.917gcm−3?
View Solution0.27 g of a long chain fatty acid was dissolved in 100cm3 of hexane. 10 mL of this solution was added dropwise to the surface of water in a round watch glass. Hexane evaporates and a monolayer is formed. The distance from edge to centre of the watch glass is 10 cm. The height of the monolayer is 10−x m. what is numerical value of x ? [Density of fatty acid =0.9gcm−3,π=3 ]
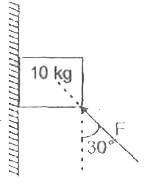
View SolutionA block of mass 10 kg is held at rest against a rough vertical wall [μ=0.5] under the action a force F as shown in figure. The minimum value of F required for it is (g=10m/s2)
 View Solution
View SolutionA cube of ice of side length 10 cm is floating in water of density 1000 kg/m3. Then pick up the correct statement (density of ice = 900 kg/m3)
View Solution

