A LASER is source of very intense, monochromatic, and unidirectional beam of light. These properties of a laser light can be exploited to measure long distance. The distance of the moon from the Earth has been already determine very precisly at the moon's surface. How much is the radius of the lunar orbit around the Earth?
We known that speed of laser light =c=3×108m/s. If d be the distance of Moon from the earth, the time taken by laser signal to return after reflection at the Moon's surface
t=2.56s=2dc=2d3×108ms−1
⇒d=12×2.56×3×108m=3.84×108m.
Topper's Solved these Questions
Similar Questions
A telescope of aperture diameter 5m is used to observe the moon from the earth. Distance between the moon and earth is 4×105 km. Determine the minimum distance between two points on the moon's surface which can be resolved using this telescope. (Wave length of light is 5893A∘.
View SolutionA telescope of aperture diameter 5m is used to observe the moon from the earth. Distance between the moon and earth is 4×105 km. Determine the minimum distance between two points on the moon's surface which can be resolved using this telescope. (Wave length of light is 5893A∘.
View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the percentage intensity of the reflected light to the intensity of the reflectd light to the intensity of incident light?

View SolutionA rocket rises vertically up from the surface of earth so that it is distance veries from the earth's surface as l=bt2 where 'b' is a constant. After 10sec the rocket has travelled 2Km. Determine it's speed at that moment.
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
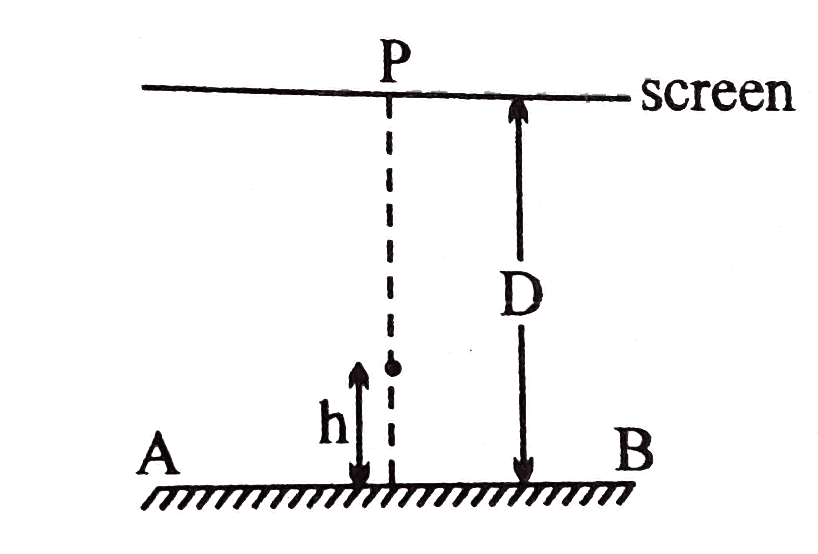
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the shape of interference fringes on the screen?

View SolutionA laser beam is sent to the moon and reflected back to earth by a mirror placed on the moon by an astronaut. If the moon is at 3,84,000 km distance from earth, how long does it take the light to make the round trip?
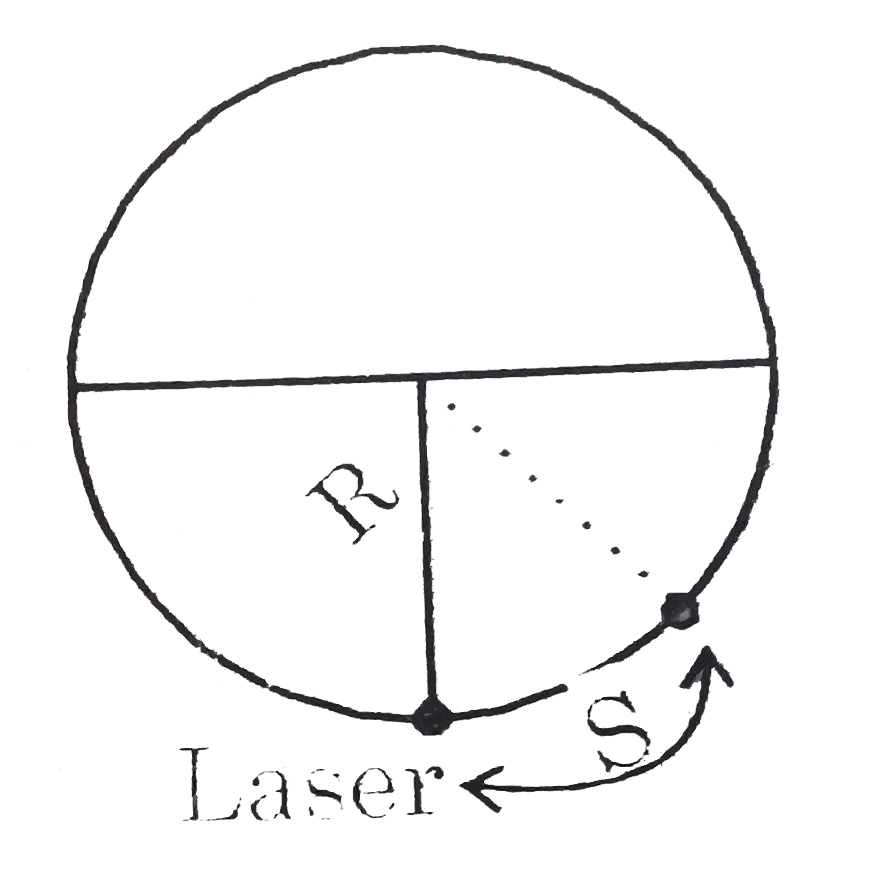
View SolutionA horizontal cylinderical tank 6πm in diameter is half full of water. The space above the water is filled with a pressurized gas of unknown refractive index. A small laser can move along the curved bottom of the water and aims a light beam towards the centre of the water surface. When the laser has moved a distance s=1m or more (measured from curved face) from the lowest point in water, no light enters the gas. The refractive index of gas is (μwater=4/3)
View SolutionThe nearest star from our solar system is 4.29 light year away. How much is this distance in terms of par sec? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the earth six months apart in its orbit around the sun?
View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. If the intensity of P correspoonds to a maximum, calculate the minimum distance through which the reflecting surface AB should so that intensity at P again becomes maximum.

View Solution