A lens forms real image of an object 20 cm away from lens. A second lens is kept in contact with this lens, then image shifts 10 cm towards the lens combination. Find the power of another lens.
To solve the problem step by step, we can follow these steps:
Step 1: Understand the Given Information
We have a lens (let's call it Lens 1) that forms a real image of an object placed 20 cm away from it. When a second lens (Lens 2) is placed in contact with Lens 1, the image shifts 10 cm towards the lens combination.
Step 2: Define Variables
- Let the object distance for Lens 1 be u=−20 cm (the negative sign is used because the object is on the opposite side of the light direction).
- The initial image distance for Lens 1 is v1=20 cm.
- The new image distance after placing Lens 2 is v2=20−10=10 cm.
Step 3: Use the Lens Formula for Lens 1
The lens formula is given by:
1f=1v−1u
For Lens 1:
1f1=1v1−1u
Substituting the values:
1f1=120−1−20
1f1=120+120=220=110
Thus, the focal length of Lens 1 is:
f1=10 cm
Step 4: Use the Lens Formula for the Combination of Lenses
For the combination of the two lenses, we have:
1f=1f1+1f2
Where f is the effective focal length of the combination. Since the new image distance is v2=10 cm, we can write:
1f=1v2−1u
Substituting the values:
1f=110−1−20
1f=110+120
Finding a common denominator (20):
1f=220+120=320
Thus, the effective focal length f is:
f=203 cm
Step 5: Substitute Back to Find f2
Now substituting back into the lens formula for the combination:
1f=1f1+1f2
320=110+1f2
Rearranging gives:
1f2=320−220=120
Thus, the focal length of Lens 2 is:
f2=20 cm
Step 6: Calculate the Power of Lens 2
The power P of a lens is given by:
P=1f (in meters)
Converting f2 to meters:
f2=20 cm=0.2 m
Thus,
P=10.2=5 diopters
Final Answer
The power of the second lens is +5 diopters.
---
We have a lens (let's call it Lens 1) that forms a real image of an object placed 20 cm away from it. When a second lens (Lens 2) is placed in contact with Lens 1, the image shifts 10 cm towards the lens combination.
- Let the object distance for Lens 1 be u=−20 cm (the negative sign is used because the object is on the opposite side of the light direction).
- The initial image distance for Lens 1 is v1=20 cm.
- The new image distance after placing Lens 2 is v2=20−10=10 cm.
The lens formula is given by:
1f=1v−1u
For Lens 1:
1f1=1v1−1u
Substituting the values:
1f1=120−1−20
1f1=120+120=220=110
Thus, the focal length of Lens 1 is:
f1=10 cm
For the combination of the two lenses, we have:
1f=1f1+1f2
Where f is the effective focal length of the combination. Since the new image distance is v2=10 cm, we can write:
1f=1v2−1u
Substituting the values:
1f=110−1−20
1f=110+120
Finding a common denominator (20):
1f=220+120=320
Thus, the effective focal length f is:
f=203 cm
Now substituting back into the lens formula for the combination:
1f=1f1+1f2
320=110+1f2
Rearranging gives:
1f2=320−220=120
Thus, the focal length of Lens 2 is:
f2=20 cm
The power P of a lens is given by:
P=1f (in meters)
Converting f2 to meters:
f2=20 cm=0.2 m
Thus,
P=10.2=5 diopters
The power of the second lens is +5 diopters.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (A. MULTIPLE CHOICE QUESTIONS)
40 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS)
21 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Long Answer Questions)
20 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A real image of an object is formed at a distance of 20cm from a lens. On putting another lens in contact with it, the image is shifted 10cm towards the combination, Determine the power of the second lens.
View SolutionRay coming from an object situated at infinity, fall on a convex lens and an image is formed at a distance of 16 cm from the lens. When a concave lens is kept in contact with the convex lens, the image is formed at a distance of 20 cm from the lens combination. Calculate the focal length of the concave lens.
View Solution
Knowledge Check
A convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
A13 cmB24 cmC33 cmD40 cmA lens forms a real image of an object. The distance from the object to the lens is x cm and that from the lens to the image is y cm. The graph shows the variation of y with x.
It can be deduced that the lens is
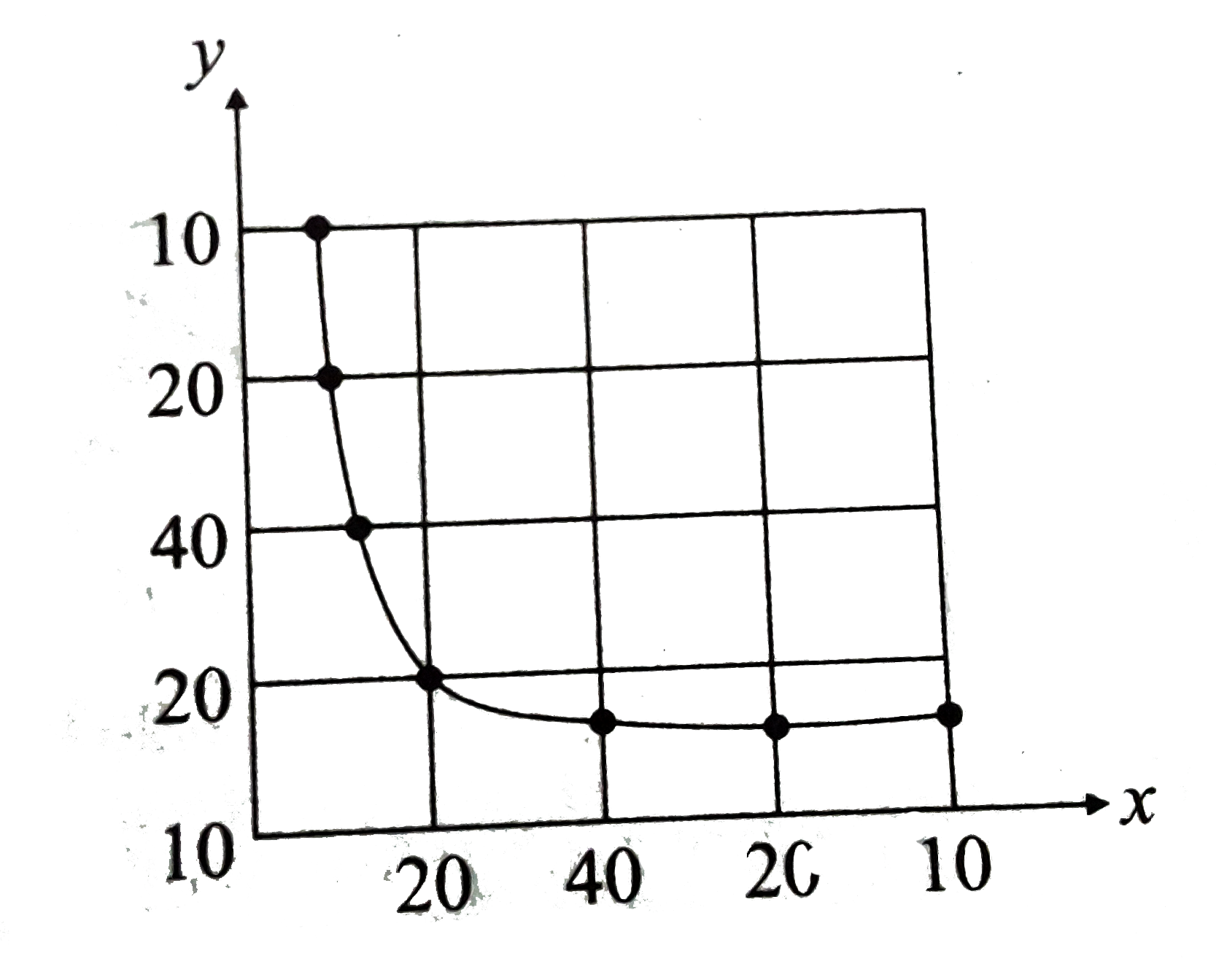 Aconverging and of focal length 10cmBconverging and of focal length 20cmCconverging and of focal length 40cmDdiverging and of focal length 20cm
Aconverging and of focal length 10cmBconverging and of focal length 20cmCconverging and of focal length 40cmDdiverging and of focal length 20cmA convex lens forms an image of an object placed 20cm away from it at a distance of 20cm on the other side of the lens. If the object is moves 5cm toward the lens, the image will be
A5cm toward the lensB5cm away from the lensC10cm toward the lensD10cm away from the lens
A point object is placed at a distance of 15 cm from a convex lens. The image is formed on the other side at a distance of 30 cm from the lens. When a concave lens is placed in contact with the convex lens, the image shifts away further by 30 cm. Calculate the focal lengths of the two lenses.
View SolutionAn object is kept at 60 cm in front of a convex lens. Its real image is formed at 20 cm from the lens . Find the focal length and power of the lens.
View SolutionA point object is placed at a distance of 15 cm from a convex lens. The image is formed on the other side of lens at a distance 30 cm from lens. When a concave lens is placed in contact with convex lens, image is shifted away further by 30 cm. calculate the focal lengths of the two lenses.
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of foal length 25 cm. The power of the lens combination is
View SolutionA convex lens forms an image of a distant object at distance of 20 cm from it. On keeping another lens in contact with the first, if the image is formed at a distance of 403 cm from the combination, then the focal length of the second lens is
View Solution
