A light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
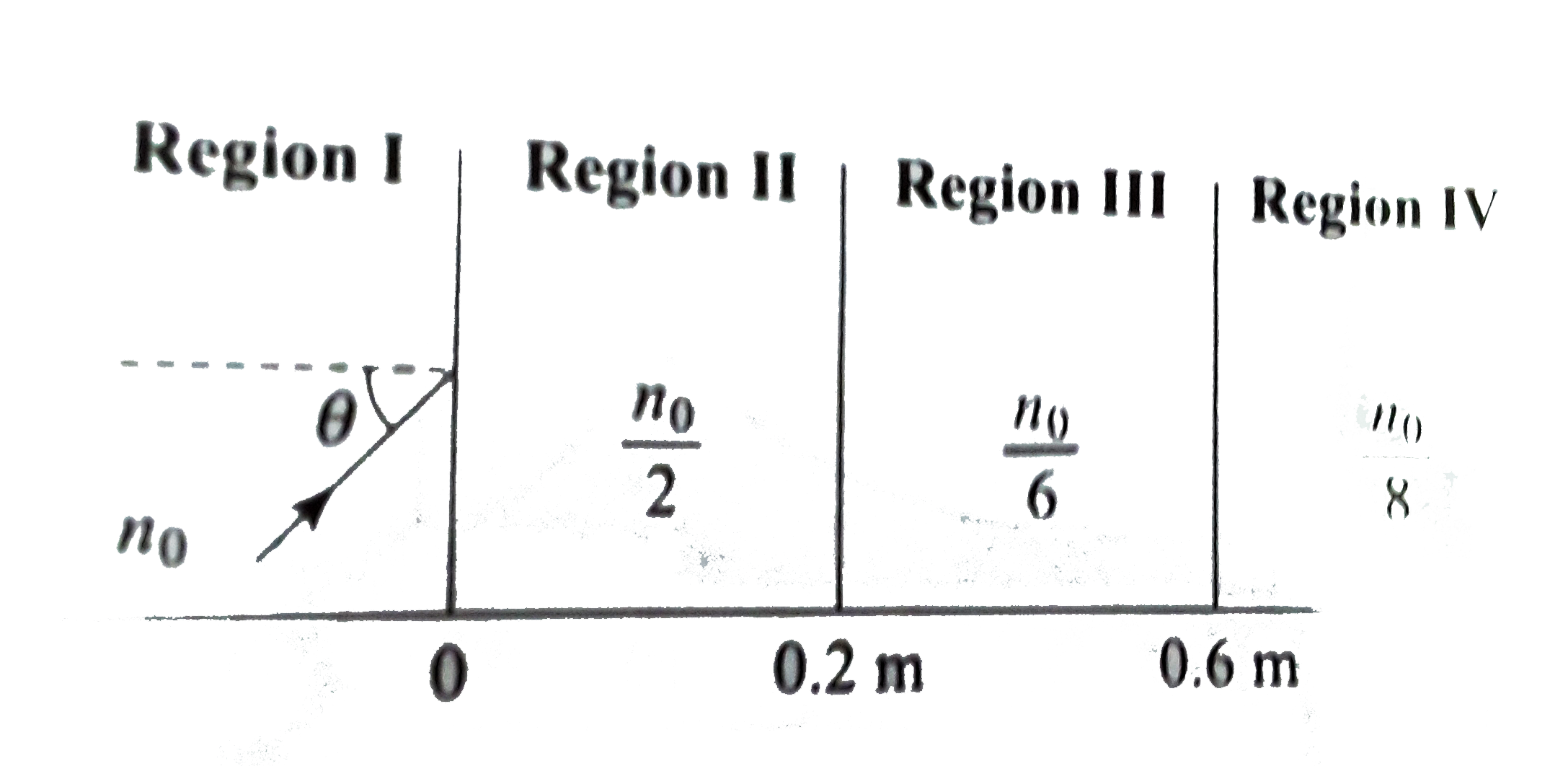
sin1(3/4)
sin1(1/8)
sin1(1/4)
sin1(1/3)
The correct Answer is:B
First of all observe that refractive index is depressing towards region IV and hence light ray is bending away from normal.
Light ray just misses to enter region IV, means that angle of refraction in region IV becomes 90∘ . We can write Snell.s law as follows :
μsinθ = constant
⇒n0sinθ=n0θsin90∘
⇒sinθ=18
⇒θ=sin−1(18)
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (C. MULTIPLE CHOICE QUESTIONS)
25 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
40 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
For a prism angle θ=600 the refractive indices of the left half and right half are resp, n1 and n2 (n2gen1) as shown in figure. The angle of incidence i is chosen such that the incident light rays will have minimum deviation if n1 = n2 = n = 1.5. For case of unequal refractive indices n1 = n and n2=n+∂at(n) the angle of emergence e=i+δ(e). Which of the following statement is/are correct?
View SolutionA parallel beam of monochromatic light of frequency v is incident on a surface. Intensity of the beam is I and area of the surface is A. Find the force exerted by the light beam on the surface for following cases–
(i) the surface is perfectly absorbing and the light beam is incident normally on it.
(ii) the surface is perfectly reflecting and the light beam is incident normally.
(iii) the surface is perfectly absorbing and the light beam is incident at an angle of incidence θ.
(iv) the surface is perfectly reflecting and the light beam is incident at an angle of incidence θ.
View Solution
Knowledge Check
A light beam is travelling from Region I to IV (figure). The refractive index in regionals I,II,III and IV are n0=n02(n_0)/(6) and (n_0)/(8)respectively.The∠of∈cncethetaforwhichthebeamjustmissesenter∈gregionIVis−
 Asin−1(34)Bsin−1(18)Csin−1(14)Dsin−1(13)
Asin−1(34)Bsin−1(18)Csin−1(14)Dsin−1(13)A beam of light passes from medium 1 to medium 2 to medium 3 as shown figure. What may be concluded about the three indices of refraction, n1,n2,andn3 ?
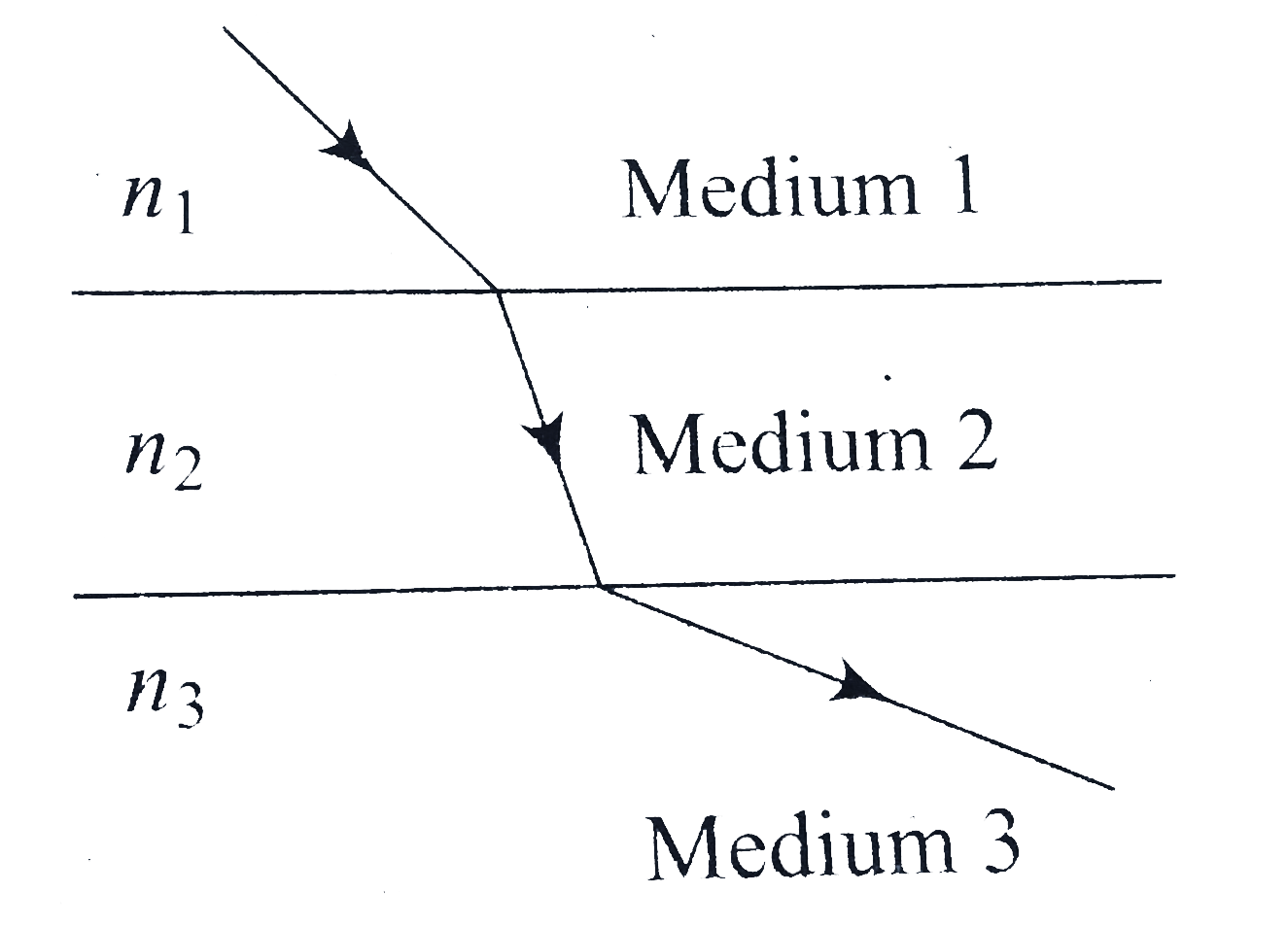 An3>n1>n2Bn1>n3>n2Cn2>n3>n1Dn2>n1>n3
An3>n1>n2Bn1>n3>n2Cn2>n3>n1Dn2>n1>n3An intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
As the beam enters the medium, it willAconvergeBdiverge near the axis and converge near the peripheryCtravel as a cyclindrical beamDdiverge
A fine pencil of β-particles, moving with a speed v, enters a region (region I), where a uniform electric field and a uniform magnetic field are both present. These β-particles then move into region II where only the magnetic field, (out of the two fields present in region I) exists. The path of the β-particles, in the two regions is as shown in the figure.
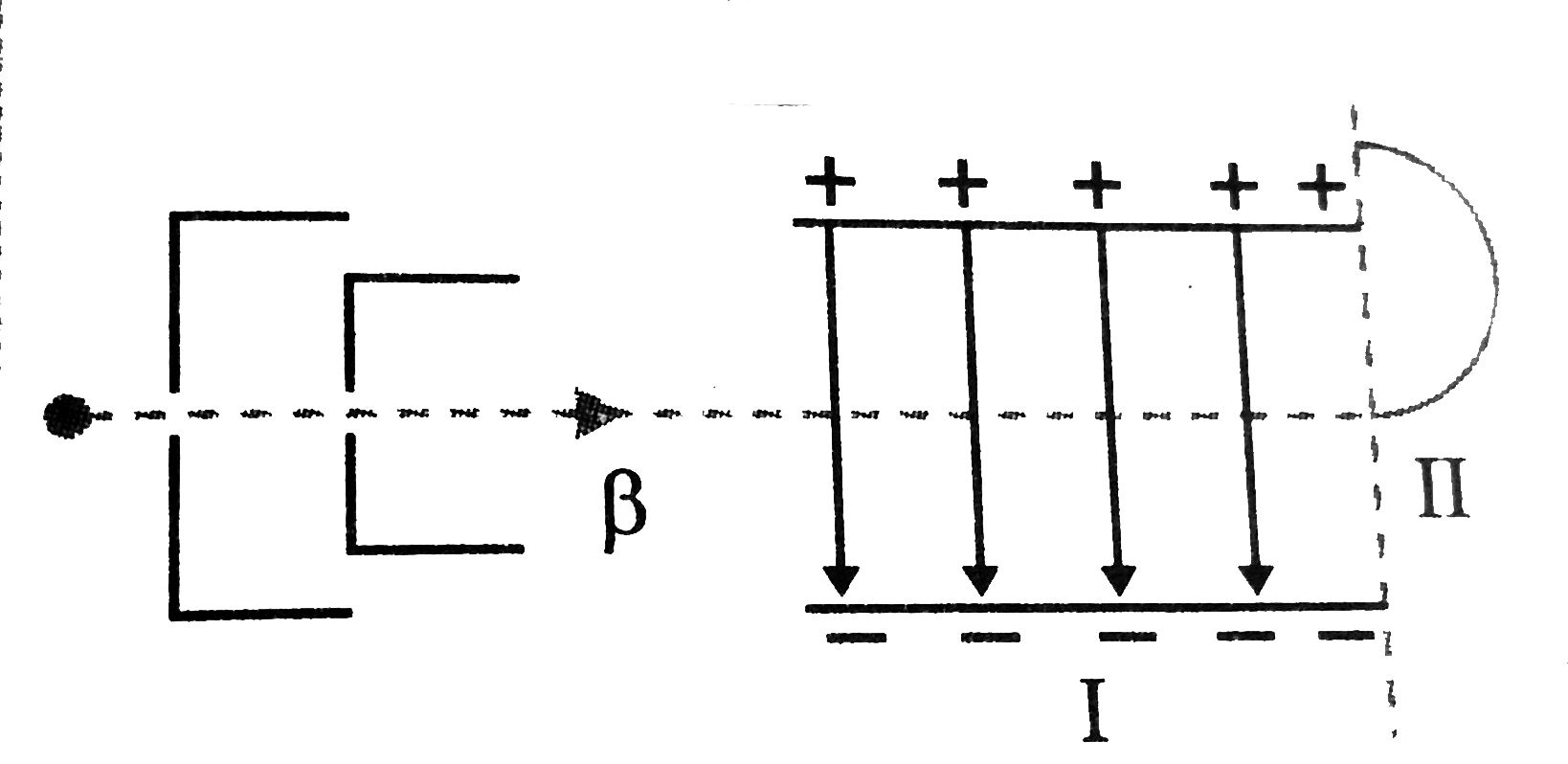
(i) state the direction of magnetic field.
(ii) state the relation between E and B in region I.
(iii) Drive the expression for the radius of the circular path of the β-particle in region II.
(iv) If the magnitude of magnetic field, in region II is changed to n times its earlier value, (without changing the magnetic field in region I) find the factor by which the radius of this circular path would change.
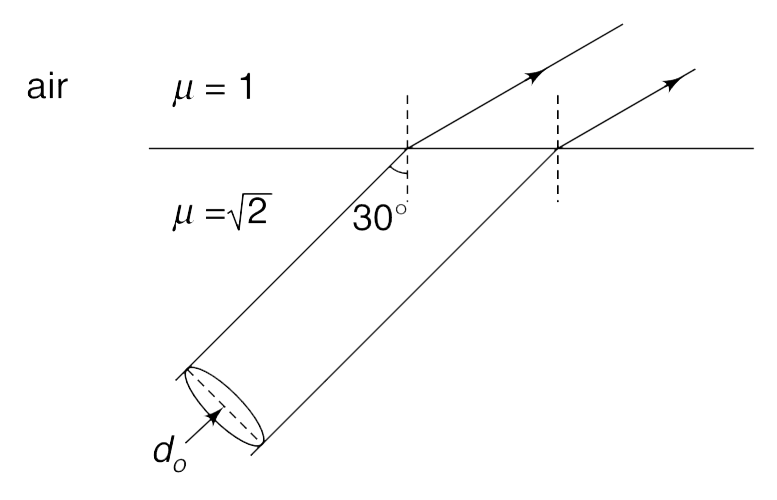
View SolutionIntensity of a light beam can be defined as amount of light energy incident in unit time on a unit area held normal to the direction of beam. A light beam of intensity I0 has a circular cross section of diameter d0. This beam is travelling in a medium of refractive index μ=√2and gets incident on the medium – air boundary at an angle of incidence i=30°. Assume that entire light energy gets transmitted into air. Find the intensity (I) of transmitted light beam.
View SolutionA monochromatic beam of light is incident at the interface of two materials of refractive index n1 and n2 as shown . If n1>n2 and θC is the critical angle then which of the following statements is NOT true ?
View SolutionA light beam travelling along the x axis with planar wavefront is incident on a medium of thickness t. In the region, where light is falling the refractive index can be taken to be varying such that dndy>0. The light beam on the other side of the medium will emerge
View SolutionA ray of light travels from a medium of refractive index n1 to
a medium of refractive index n2. If angle of incidence is i and
angle of refraction is r, than sinisinr is equal to
View Solution

