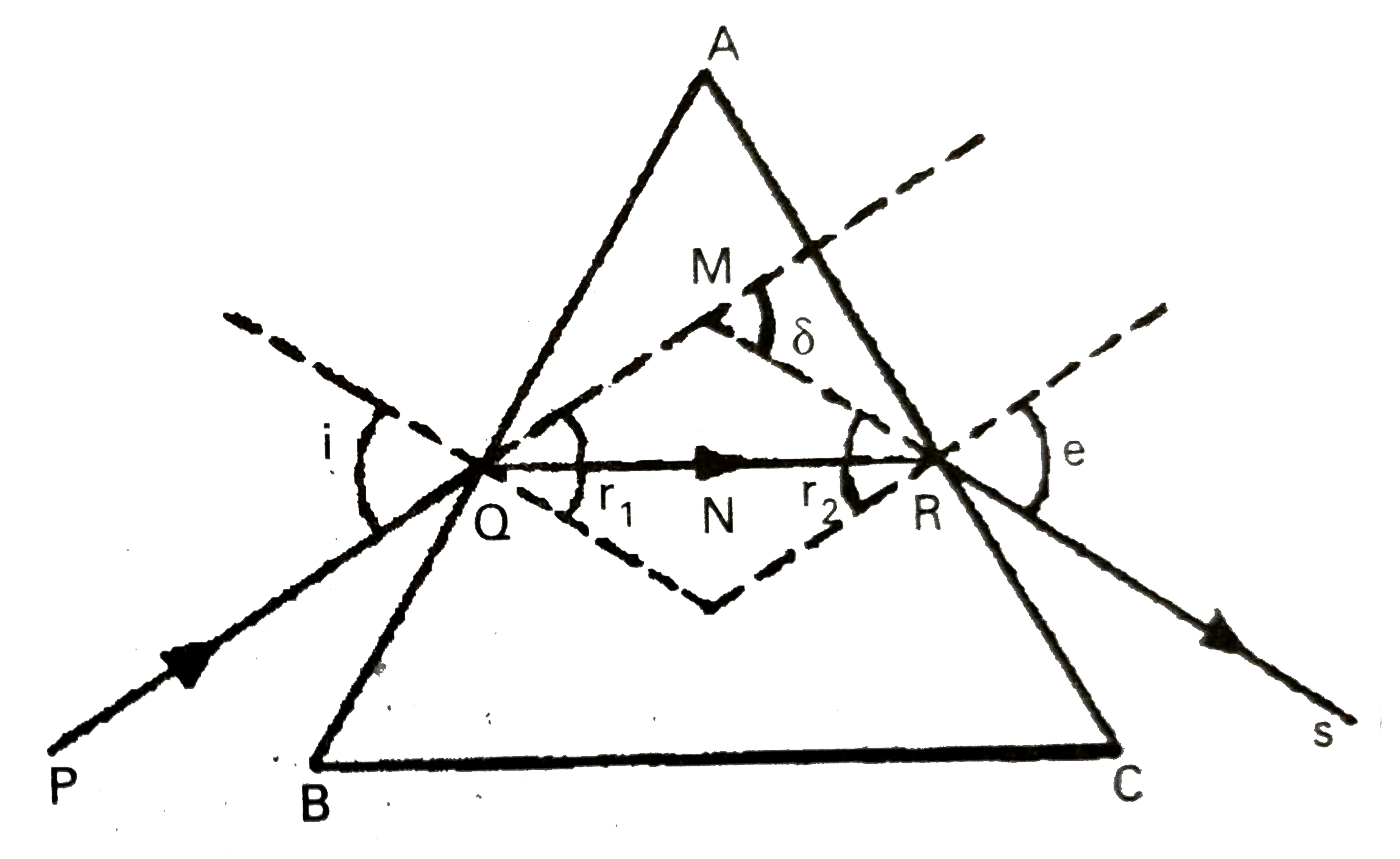
A light ray passes through a prism of angle A in a position of minimum deviation. Obtain and expression for (a) the angle of incidence in terms of the angle of the prism and the angle of minimum deviation (b) the angle of refraction in terms of the refractive index of the prism.

Text Solution

Verified by Experts

In the quadrilateral AQNR
$∠ A + ∠ Q N R = 180^{\circ} \dots\dots\dots\dots\dots\dots\dots\dots\dots..(1)$
From $Δ^{le}$ QNR, $r_{1} + r_{2} + ∠ Q N R = 180^{\circ} \dots\dots\dots\dots\dots\dots\dots\dots\dots..(2)$
$r_{1} + r_{2} = A \dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots(3)$
$Total deviation δ = (i - r_{1}) + (e - r_{2})$
$δ = i + e - A ....................(4)$
(a) At minimum deviatoin position $δ = D_{m}, i = e and r_{1} = r_{2} = r$
$∴ From eq (4), D_{m} = 2 i - A$
$i = \frac{A + D_{m}}{2} ......................(5)$
(b) From eq (3), $r + r = A$
$r = A / 2 ..........................(6)$
Refractive index of hte prism $μ = \frac{sin i}{sin r} ............................(7)$
$sin r = \frac{sin i}{μ}, r = {sin}^{- 1} (\frac{sin i}{μ})$
$μ = \frac{sin (\frac{A + D_{m}}{2})}{sin A / 2} .........................(8)$

Updated on:21/07/2023

A ray passes through a prism of angle $60^{\circ}$ in minimum deviation position and suffers a deviation of $30^{\circ}$ . What is the angle of incidence on the prism
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
If a prism having refractive index $\sqrt{2}$ has angle of minimum deviation equal to the angle of refraction of the prism, then the angle of refraction of the prism is:
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$