A liquid solution of coefficient of viscosity 2×10−3Nsm−2 made to drive with velocity of 10−4 m/s along the Xylem vessels of radius 3/4 m and length 7cm. Calculate the pressure difference across the length of Xylem vessel.
The correct Answer is:19.9×10−12 pascal
To calculate the pressure difference across the length of the xylem vessel, we can use Poiseuille's Law, which relates the flow of a viscous fluid through a cylindrical pipe. The formula is given by:
Q=πPr48ηL
Where:
- Q is the volumetric flow rate,
- P is the pressure difference,
- r is the radius of the pipe,
- η is the coefficient of viscosity,
- L is the length of the pipe.
Step 1: Convert all units to SI units
- Coefficient of viscosity, η=2×10−3N s/m2
- Velocity, V=10−4m/s
- Radius, r=34m=0.75m
- Length, L=7cm=0.07m
Step 2: Calculate the cross-sectional area A
The cross-sectional area A of the xylem vessel can be calculated using the formula for the area of a circle:
A=πr2
Substituting the radius:
A=π(0.75)2=π×0.5625≈1.7671m2
Step 3: Relate volumetric flow rate Q to velocity and area
The volumetric flow rate Q can also be expressed as:
Q=A⋅V
Substituting the values:
Q=1.7671m2×10−4m/s≈1.7671×10−4m3/s
Step 4: Rearranging Poiseuille's Law to find pressure difference P
We can rearrange Poiseuille's Law to solve for P:
P=8ηLQπr4
Step 5: Calculate r4
First, calculate r4:
r4=(0.75)4=0.3164m4
Step 6: Substitute all values into the equation for P
Now substitute the values into the rearranged equation:
P=8×(2×10−3)×(0.07)×(1.7671×10−4)π×0.3164
Calculating the numerator:
Numerator=8×2×10−3×0.07×1.7671×10−4≈1.0007×10−7
Calculating the denominator:
Denominator=π×0.3164≈0.9932
Now calculate P:
P≈1.0007×10−70.9932≈1.0075×10−7Pascals
Final Result
The pressure difference across the length of the xylem vessel is approximately:
P≈1.0075×10−7Pascals
- Q is the volumetric flow rate,
- P is the pressure difference,
- r is the radius of the pipe,
- η is the coefficient of viscosity,
- L is the length of the pipe.
- Coefficient of viscosity, η=2×10−3N s/m2
- Velocity, V=10−4m/s
- Radius, r=34m=0.75m
- Length, L=7cm=0.07m
The cross-sectional area A of the xylem vessel can be calculated using the formula for the area of a circle:
The volumetric flow rate Q can also be expressed as:
We can rearrange Poiseuille's Law to solve for P:
First, calculate r4:
Now substitute the values into the rearranged equation:
The pressure difference across the length of the xylem vessel is approximately:
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Problems
9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
in a plate, a sucrose solution of coefficient of visocity 1.5×10−3Nsm−2 is driven at a velocity of 10−3ms−1 throught x ylem vessel of radius 2μ m and length5μm. Find the hydrostatic pressure difference across the length of xylem vessel.
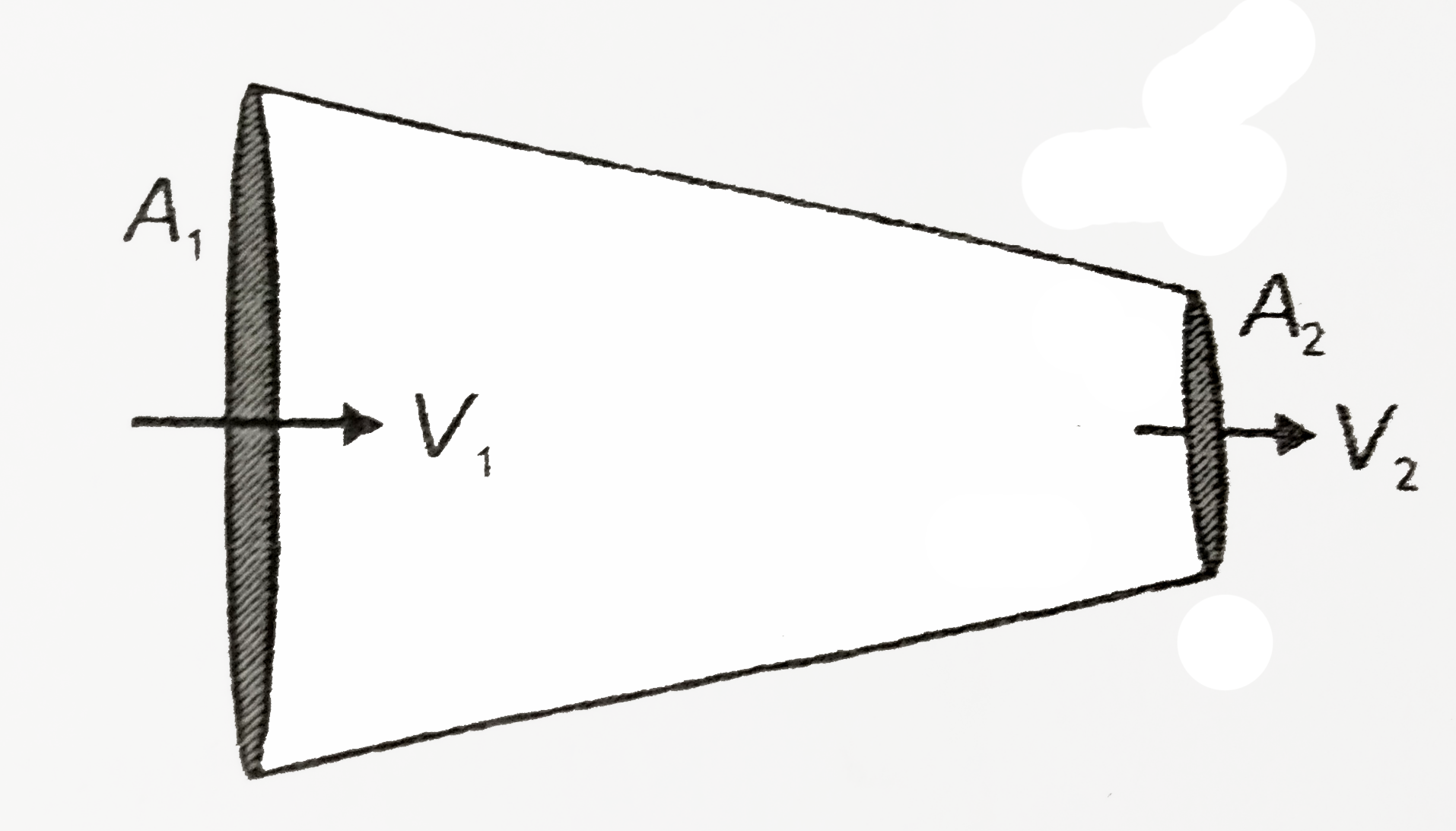
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
View Solution
Knowledge Check
The workdone by pressure in forcing 1m3 of water through a pipe if the pressure difference across the pipe is 104 Pa, is
A105JB104JC103JD102J
A liquid of density 103kgm3 and coefficient of viscosity 8 xx10^(-2) decapoise is flowing in a tube of radius 2 cm with speed 2 m/s. The. Reynold’s number is
View SolutionCalculate the rate of flow of glycerine of density 1.25×103kg/m3 through the conical section of a pipe if the radii of its ends are 0.1m and 0.04 m and the pressure drop across its lengths is 10N/m2.
View SolutionA steel ball of density 8.0×103kg/m3 and radius 2 mm is observed to fall with a terminal velocity 1.0×10−2m/s in a liquid of density 1.8×103kg/m3 . Calculate the viscosity of the liquid.
View SolutionA barometer contains two uniform capillries of radii 1.44×10−3m and 7.2×10−4m. If the height of the liquid in the narrow tube is 0.2m more than that in the wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=m/s2.
View SolutionThe density of a gas is 6×10−2kg/m3 and the root mean square velocity of the gas molecules is 500 m/s. The pressure exerted by the gas on the walls of the vessel is
View SolutionA barometer contains two uniform capillaries of radii 1.4×10−3m and 7.2×10−4m. If the height of liquid in narrow tube is 0.2m more than that in wide tube, calculate the true pressure difference. Density of liqid =103kg/m3, surface tension =72×10−3N/m and g=9.8ms−12.
View SolutionVelocity of light in glass is 2×108m/s and that in air is 3×108m/s. Calculate the apparent shift of an ink dot covered by a 6 cm thick glass plate.
View Solution
