A load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley. 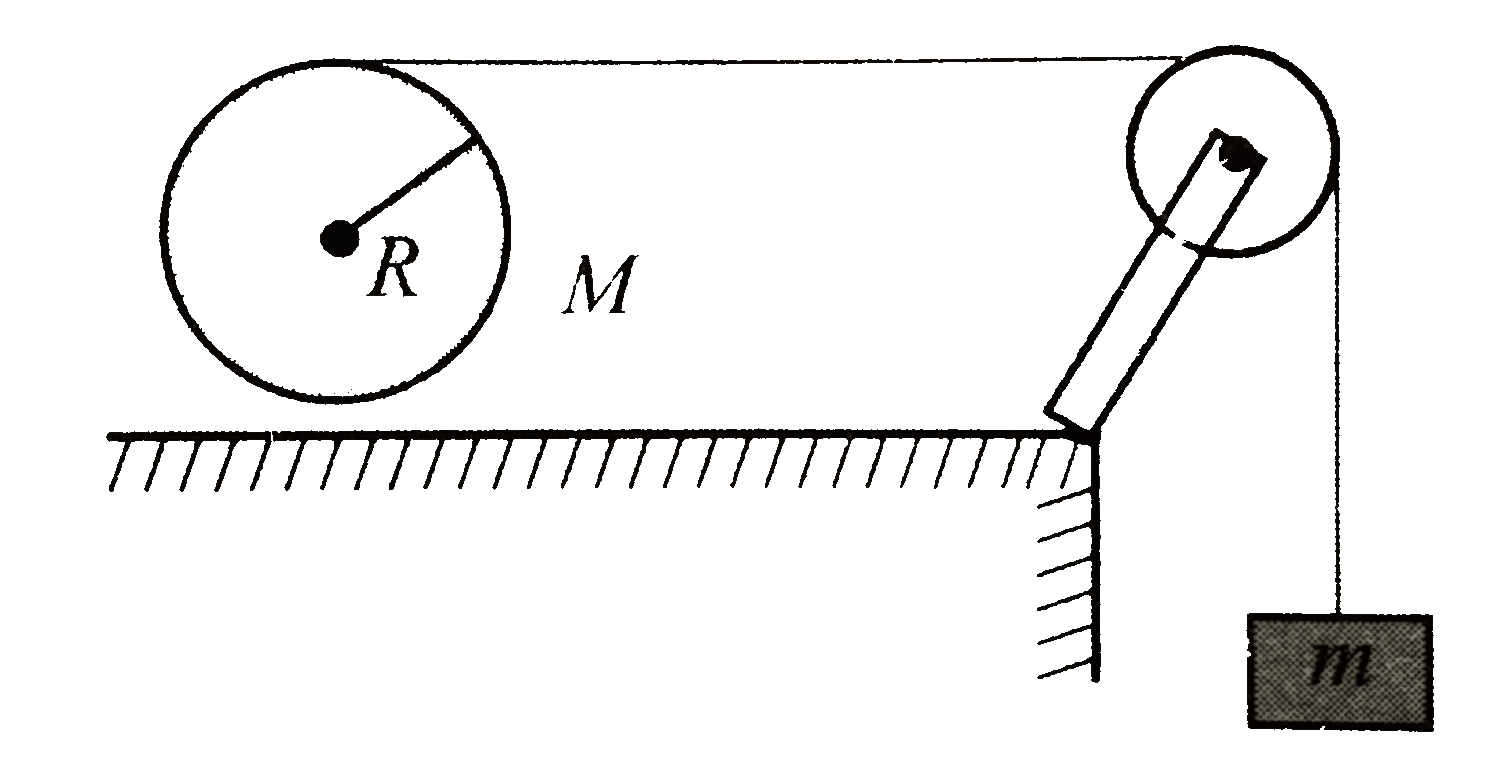
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
The cylinder will roll without slipping so long as the friction force is suficiently large and it never reaches the limiting value. The force acting on the cylinder are a. its weight Mg, b. normal reaction N, c. tension T to the right, d ffr to the right. let a be the acceleration of the falling mass ,m.
Then aCM=a2
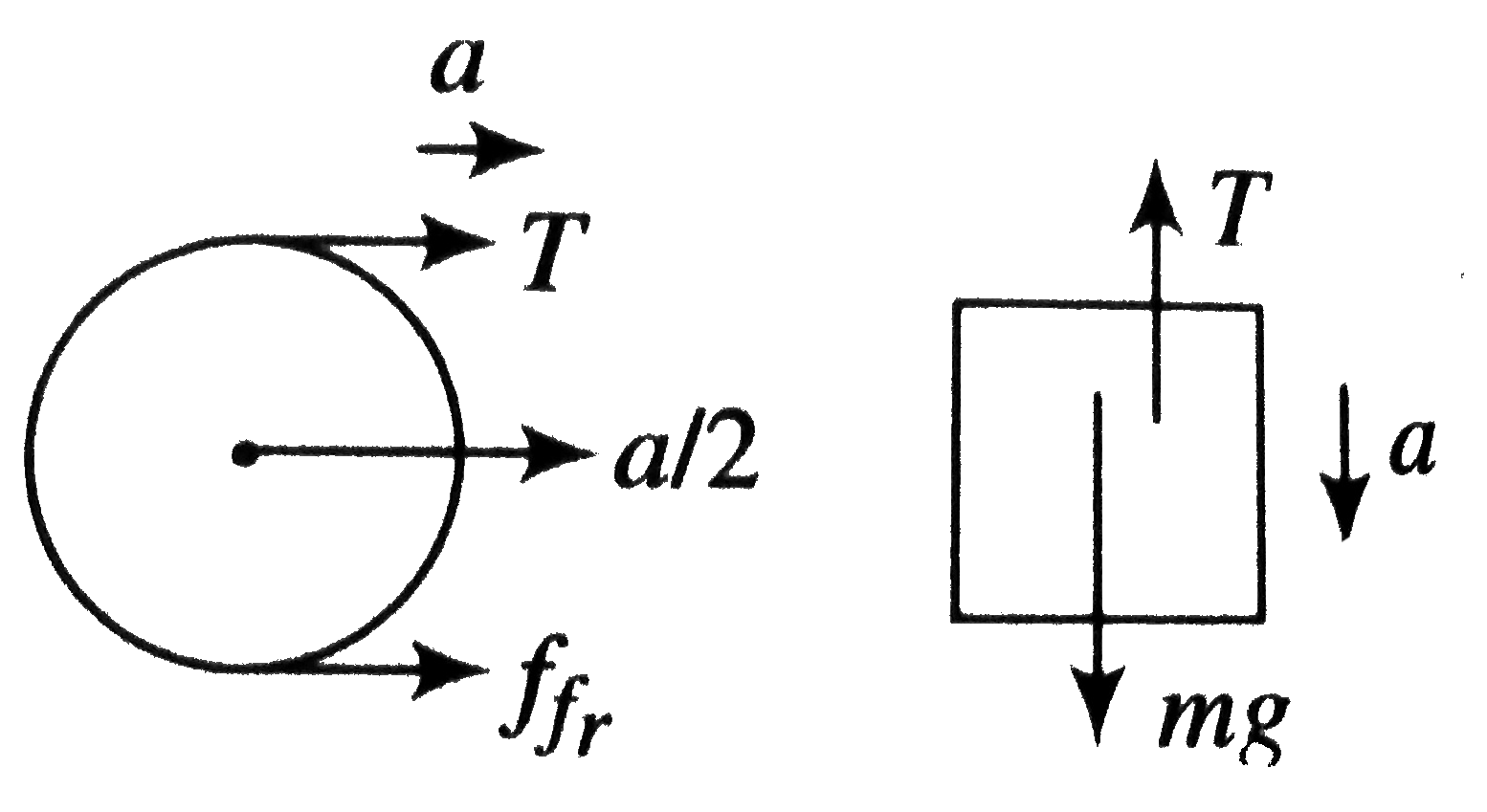
mg−T=ma
⇒T=mg−ma
For the cylinder
T+ffr=Ma2
and τ=TR−ffrR=(12MR2)α
T−ffr=12MRα=12MR(aCMR)=12MaCM=14Ma
Solving ffr=18Ma
T=38Maanda=mgm+38M
There will be no slip if
ffr≤μmg⇒μ≥Ma8mg
or μ>M8m=3M
Rolling +slipping: Now aCM≠αR, rather acceleration of the highest point of the cylinder =aCM+αR= acceleration of m.
and τ=TR−flimR=(12MR2)α
T−μMg=12MRα
For load mg−t=ma
Solving for α
a=3mg−μMgM+3m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?
 View Solution
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA spherical shell of radius R is rolling down an incline of inclination θ without slipping. Find minimum value of coefficient of friction.
 View Solution
View SolutionA cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
View SolutionDerive an expression for the acceleration of a solid cylinder rolling without slipping down an inclined plane. Also find the minimum coefficient of friction required for pure rolling
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png) View Solution
View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
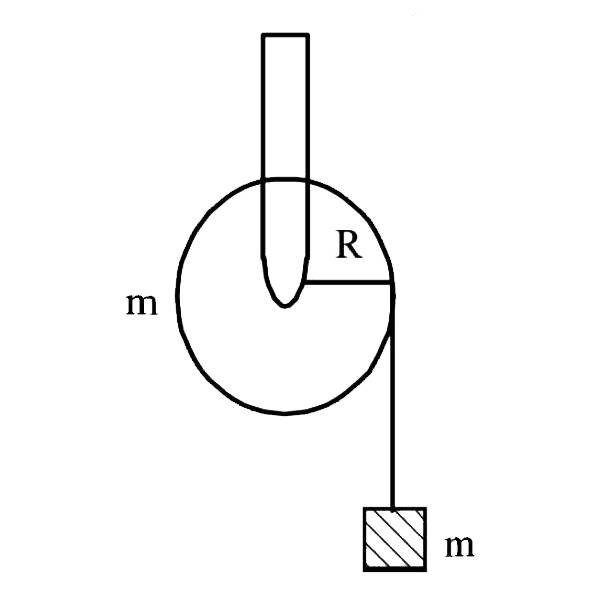 View Solution
View Solution
