A loaded 20,000kg coal wagon is moving on a level track at 6ms−1. Suddenly 5000kg of coal is dropped out of the wagon. The final speed of the wagon is
6ms−1
8ms−1
4.8ms−1
4.5ms−1
The correct Answer is:A
To solve the problem of finding the final speed of the coal wagon after dropping out some coal, we can use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Identify the initial conditions
- Mass of the coal wagon (M_initial) = 20,000 kg
- Initial velocity of the wagon (V_initial) = 6 m/s
- Mass of coal dropped (M_dropped) = 5,000 kg
Step 2: Calculate the initial momentum
The initial momentum (P_initial) of the system (wagon + coal) can be calculated using the formula:
Pinitial=Minitial×Vinitial
Substituting the values:
Pinitial=20,000kg×6m/s=120,000kg m/s
Step 3: Determine the mass of the wagon after dropping coal
After the coal is dropped, the mass of the wagon (M_final) becomes:
Mfinal=Minitial−Mdropped=20,000kg−5,000kg=15,000kg
Step 4: Calculate the momentum of the dropped coal
The momentum of the coal that was dropped can be calculated as:
Pdropped=Mdropped×Vinitial=5,000kg×6m/s=30,000kg m/s
Step 5: Apply the conservation of momentum
According to the conservation of momentum:
Pinitial=Pfinal
The final momentum consists of the momentum of the remaining wagon and the dropped coal:
Pfinal=Mfinal×Vfinal+Pdropped
Substituting the known values:
120,000kg m/s=15,000kg×Vfinal+30,000kg m/s
Step 6: Solve for the final velocity of the wagon
Rearranging the equation to solve for Vfinal:
120,000kg m/s−30,000kg m/s=15,000kg×Vfinal
90,000kg m/s=15,000kg×Vfinal
Dividing both sides by 15,000 kg:
Vfinal=90,000kg m/s15,000kg=6m/s
Conclusion
The final speed of the wagon after dropping the coal remains 6 m/s.
---
- Mass of the coal wagon (M_initial) = 20,000 kg
- Initial velocity of the wagon (V_initial) = 6 m/s
- Mass of coal dropped (M_dropped) = 5,000 kg
The initial momentum (P_initial) of the system (wagon + coal) can be calculated using the formula:
Pinitial=Minitial×Vinitial
Substituting the values:
Pinitial=20,000kg×6m/s=120,000kg m/s
After the coal is dropped, the mass of the wagon (M_final) becomes:
Mfinal=Minitial−Mdropped=20,000kg−5,000kg=15,000kg
The momentum of the coal that was dropped can be calculated as:
Pdropped=Mdropped×Vinitial=5,000kg×6m/s=30,000kg m/s
According to the conservation of momentum:
Pinitial=Pfinal
The final momentum consists of the momentum of the remaining wagon and the dropped coal:
Pfinal=Mfinal×Vfinal+Pdropped
Substituting the known values:
120,000kg m/s=15,000kg×Vfinal+30,000kg m/s
Rearranging the equation to solve for Vfinal:
120,000kg m/s−30,000kg m/s=15,000kg×Vfinal
90,000kg m/s=15,000kg×Vfinal
Dividing both sides by 15,000 kg:
Vfinal=90,000kg m/s15,000kg=6m/s
The final speed of the wagon after dropping the coal remains 6 m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective
32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion and Reason
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Find velocity of wagon as function of time when it is being filled with stationary hopper at the rate μ kg/sec. and constant force F is applied horizontally on the wagon as shown in figure.
M0 is the mass of the wagon and initial speed of the wagon u = 0 at time t = 0.
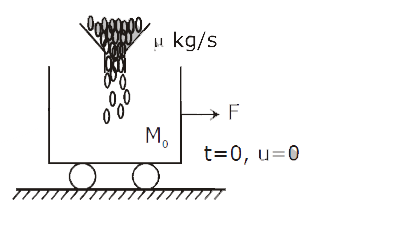
View SolutionAn open water tight railway wagon of mass 5×103kg moves at an initial velocity 1.2m/s without friction on a railway track. Rain drops fall vertically downwards into the wagon. The velocity of the wagon after it has collected103kg of water will be :-
View Solution
Knowledge Check
A wagon of 200kg is moving on a smooth track with velocity of 2m/sec. A man of 80kg also runs in the wagon with a velocity such that speed of the centre of mass of the system is zero. Find the velocity of man relative to the wagon (in m//s).
A5B6C7D8A body of mass 4kg moving with a speed of 3ms−1 collides head on with a body of mass 3kg moving in the opposite direction at a speed of 2ms−1. The first body stops after the collision. The final velocity of the second body is
A3ms−1B5ms−1C−9ms−1D30ms−1An open water tight railway wagon of mass 5×10(3)kg coats at an initial velocity 1.2m/s without friction on a railway track. Rain drops fall vertically downwards into the wagon. The velocity of the wagon after it has collected103kg of water will be :-
A0.5m/sB2m/sC1m/sD1.5m/s
An empty truck of mass 1000 kg is moving at a speed of 36 km h−1. It is loaded with 500 kg material on its way and again moves with the same speed. Will the momentum of the truck remain the same after loading? If not, find the momentum of the truck after loaded.
View SolutionTwo bodies of masses 2 kg and 1 kg are moving along the same line with speeds 2ms−1 and 5ms−1 respectively. What is the speed of the centre of mass of the system if the two bodies are moving (i) in same direction and (ii) in opposite directions?
View SolutionA 8000kg engine pulls a train of 5wagons, each of 2000kg, along a horizontal track. If the engine exerts a force of 40000N and the track offers a frictional force of 5000N, then calculate:
(a) the net accelerating force, (b) the acceleration of the train, and
(c ) the force of wagon 1 on wagon 2.
View SolutionA truck of mass 500kg is moving with constant speed 10ms−1. If sand is dropped into the truck at the constant rate 10kgmin,the force required to mainatain the motion with constant velocity is .
View SolutionA body of mass 1000 kg is moving horizontally with a velocity 50 ms−1. A mass of 250 kg is added. Find the final velocity.
View Solution
