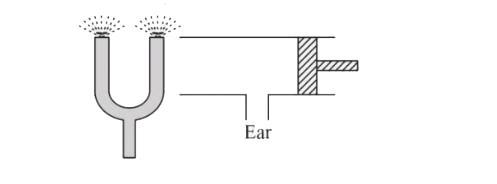
A long cylindrical tube carries a highly polished piston and has a side opening . A tuning fork of frequency $n$ is sounded at the open end of the tube . The intensity of the sounded heard by the listener changes if the piston is moved in or out. At a particular position of the piston he hears a maximum sound . When the piston is moved through a distance of $9 c m$ , the intensity of sound becomes minimum. If the speed of sound is $360 m / s$ , the value of $n$ is

A

$129.6 H z$

B

$500 H z$

C

$1000 H z$

D

$2000 H z$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

When piston moves a distance $x_{1}$ , path difference changes by $2 x$ .
Therefore , the path difference between maxima and consecutive minima $= λ / 2$
$2 x = λ / 2$
or $λ = 4 x = 4 \times 9 c m = 36 c m = 0.36 m$
$n = \frac{v}{λ} = \frac{360}{0.36} = 1000 H z$

Updated on:21/07/2023

|

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Vibrating tuning fork of frequency $n$ is placed near the open end of a long cylindrical tube. The tube has a side opening and is fitted with a movable reflecting piston. As the piston is moved through $8.75 c m$ , the intensity of sound changes from a maximum to minimum. If the speed of sound is $350 m / s$ . Then $n$ is

A500 Hz
B1000 Hz
C2000 Hz
D4000 Hz

CENGAGE PHYSICS ENGLISH-SUPERPOSITION AND STANDING WAVES-Single Correct

Home
Ask Doubt
Profile