A long rod has one end at 0∘C and other end at a high temperature. The coefficient of thermal conductivity varies with distance from the low temperature end as K=K0(1+ax), where K0=102 SI unit and a=1m−1 . At what distance from the first end the temperature will be 100∘C? The area of cross-section is 1cm2 and rate of heat conduction is 1 W.
2.7 m
1.7m
3 m
1.5 m
The correct Answer is:B
H=TDR
∴R=TDH=100−01
=100kW−1
Now, R=∫x0dR=∫x0(dxK0(1+ax)A)
or 100=∫x0dx102(1+x)(10−4)
Solving this equation we get,
x=1.7m.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct
5 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Subjective
13 Videos
- BASIC MATHEMATICSBOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
A rod of length l with thermally insulated lateral surface is made of a material whose thermal conductivity varies as K=sc/T where c is a constant. The ends are kept at temperatures T1 and T2. Find the temperature at a distance x from te first end where the temperature is T1 and the heat flow density.
View SolutionA rod of length l with thermally insulated lateral surface is made of a matrical whose thermal conductivity varies as K=C/T where C is a constant The ends are kept at temperature T1 and T2 The temperature at a distance x from the first end where the temperature is T1,T=T1(T2T1)nx/2l Find the value of n? .
View Solution
Knowledge Check
A rod AB is 1m long. The temperature of its one end A is maintained at 100∘C and other end B at 10∘C, the temperature at a distance of 60 cm from point B is
A64∘CB36∘CC46∘CD72∘CA rod of length l (laterally thermally insulated) of the uniform cross sectional area A consists of a material whose thermal conductivity varies with temperature as K=K0a+bT' where K0, a and b are constants. T1 and T2(<T1) are the temperatures of the ends of the rod. Then, the rate of flow of heat across the rod is
AAK0bl(a+bT1a+bT2)BAK0bl(a+bT2a+bT1)CK0Ablln[a+bT1a+bT2]DAK0blln[a+bT2a+bT1]The end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
A16∘CB32∘CC48∘CD64∘C
A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
View SolutionHeat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
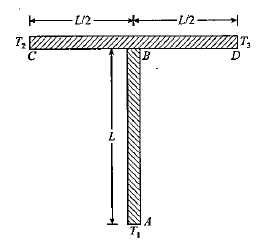
View SolutionThe ends of a cylinder steel rod are maintained at two different temperatures. The rod conducts heat from one end to the other at a rate of 10 cal/ s. At what rate would a steel rod twice as long and twice the diameter conduct heat between the same two temperatures?
View Solution
