A longitudinal standing wave $y = a cos k x cos ω t$ is maintained in a homogeneious medium of density $ρ$ . Here $ω$ is the angular speed and $k$ , the wave number and $a$ is the amplitude of the standing wave . This standing wave exists all over a given region of space.
If a graph $E (= E_{p} + E_{k})$ versus $t$ , i.e., total space energy density verus time were drawn at the instants of time $t = 0$ and $t = T / 4$ , between two successive nodes separated by distance $λ / 2$ which of the following graphs correctly shows the total energy $(E)$ distribution at the two instants.

A

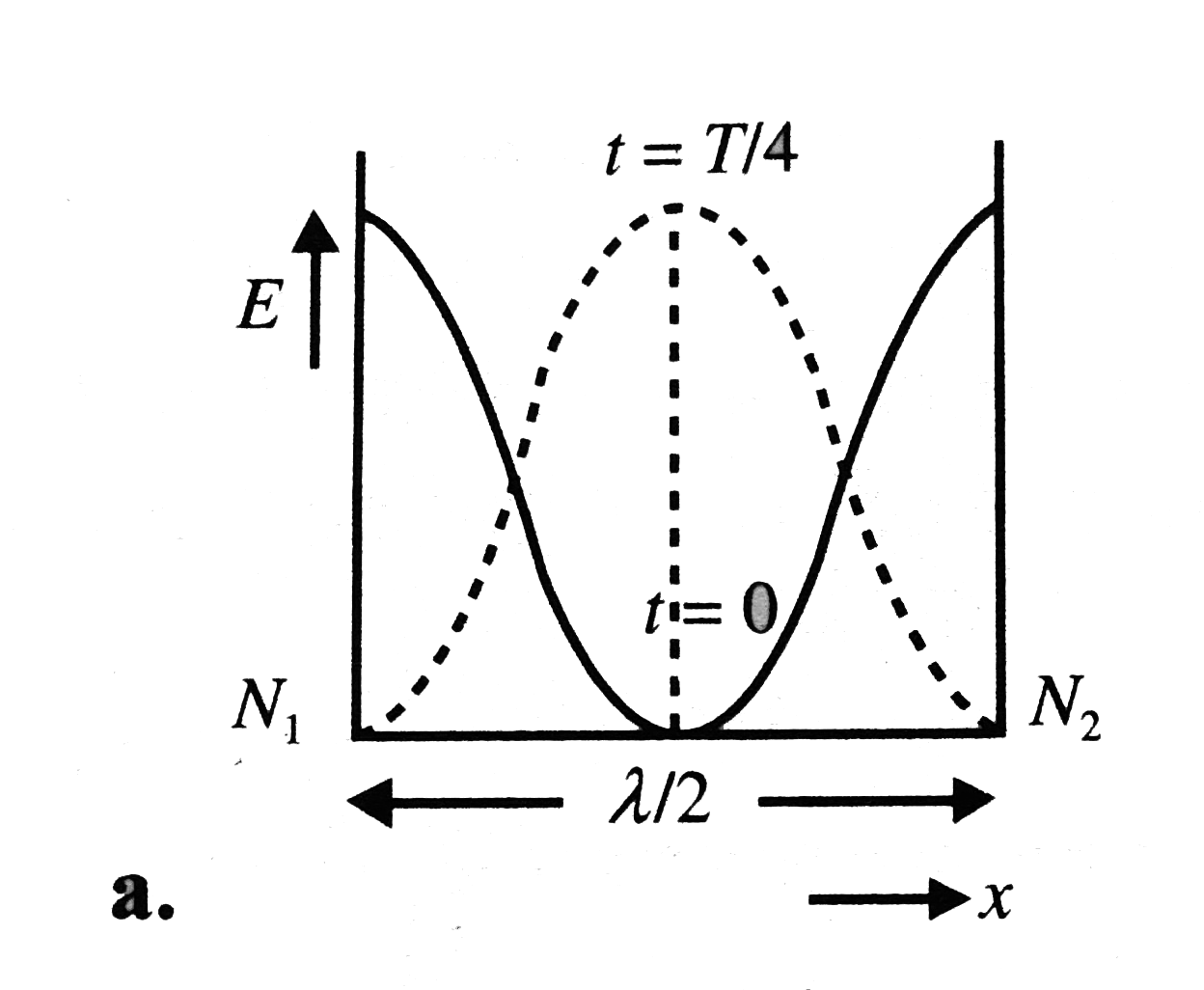
ocr_image

B

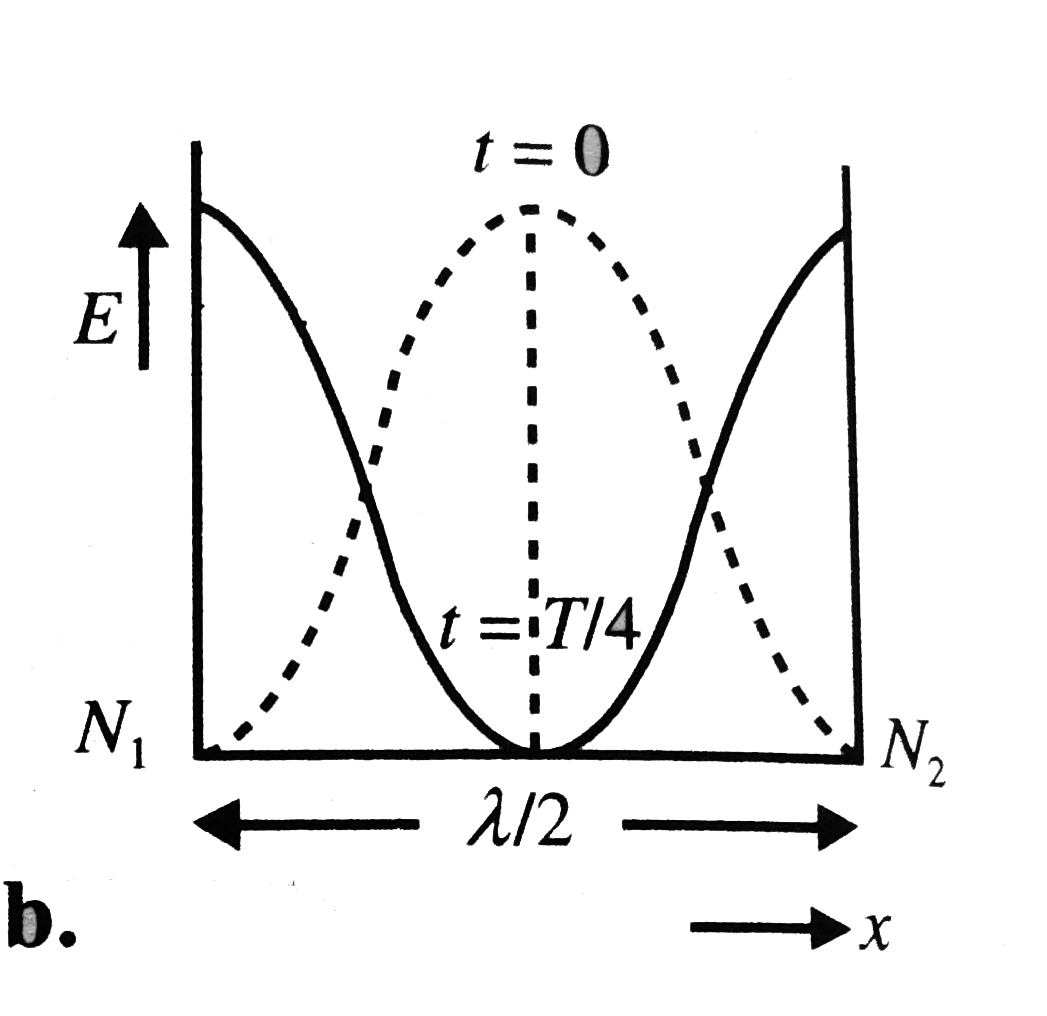
ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The graphs shown are between two successive nodes , say
$x_{1} = λ / 4 a t N_{1}$ and $x_{2} = 3 λ / 4 a t N_{2}$ .
Total energy density is
$E = E_{p} + E_{k})$
$= \frac{ρ a^{2} ω^{2}}{2} [{sin}^{2} k x {cos}^{2} ω t + {cos}^{2} k x {sin}^{2} ω t]$
Putting $x = λ / 2$ , ( first antinode)
${(E)}_{λ / 2} = \frac{ρ a^{2} ω^{2}}{2} [{sin}^{2} ω t]$
At $t = 0, {(E)}_{λ / 2} = 0$ and at $t = \frac{T}{4}$
${(E)}_{λ / 2} = \frac{ρ a^{2} ω^{2}}{2}$
This is truly reflected in the graph $(a)$ .

|

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

A longitudinal standing wave $y = a cos k x cos ω t$ is maintained in a homogeneious medium of density $ρ$ . Here $ω$ is the angular speed and $k$ , the wave number and $a$ is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . $K E = E_{k} (x, t)$ at the point $(x, t)$ is given by
A $E_{k} = \frac{ρ a^{2} ω^{2}}{2} {cos}^{2} k x {cos}^{2} ω t$
B $E_{k} = \frac{ρ a^{2} ω^{2}}{2} {sin}^{2} k x {cos}^{2} ω t$
C $E_{k} = \frac{ρ a^{2} ω^{2}}{2}$
D $E_{k} = \frac{ρ a^{2} ω^{2}}{2} {cos}^{2} k x {sin}^{2} ω t$
A longitudinal standing wave $y = a cos k x cos ω t$ is maintained in a homogeneious medium of density $ρ$ . Here $ω$ is the angular speed and $k$ , the wave number and $a$ is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy $P E = E_{p} (x, t)$ at a point $(x, t)$ in this space is
A $E_{p} = \frac{ρ a^{2} ω^{2}}{2}$
B $E_{p} = \frac{ρ a^{2} ω^{2}}{2} {cos}^{2} k x {sin}^{2} ω t$
C $E_{p} = \frac{ρ a^{2} ω^{2}}{2} {sin}^{2} k x {cos}^{2} ω t$
D $E_{p} = \frac{ρ a^{2} ω^{2}}{2} {sin}^{2} k x {sin}^{2} ω t$

CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Comprehension

Home
Ask Doubt
Profile