A loop of rope is whirled at a high angular velocityω, so that it becomes a taut circle of radiusR. A kink develops in the whirling rope. 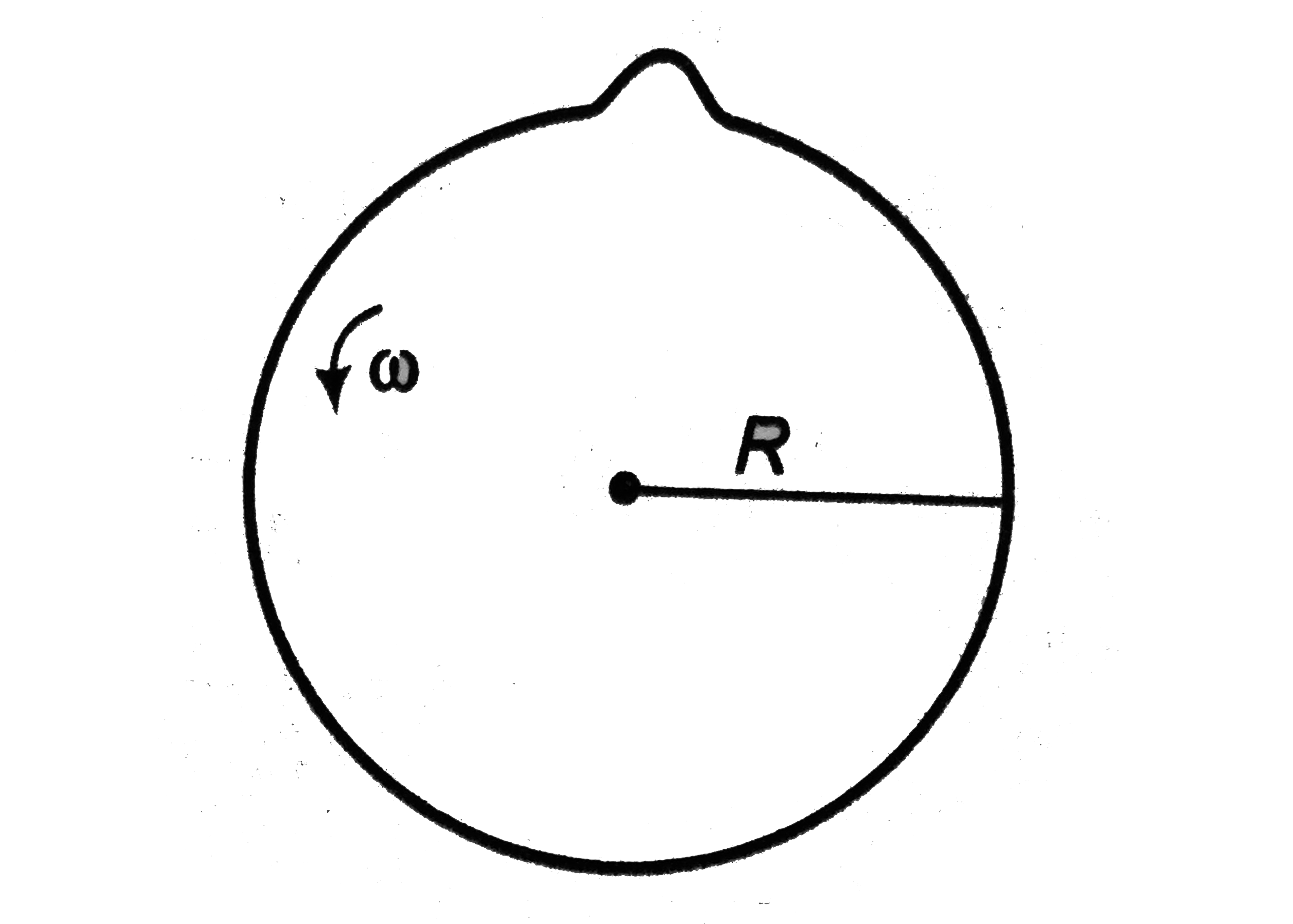
(a) Show that the speed of the kink in the rope is v=ωR.
(b) Under what conditions does the kink remains stattionary relative to an observer on the ground?
The correct Answer is:A, B, C, D
(a) Tcosdθ components are cancelled. Tsindθ components provided the necessary centriprtal force to Pθ.

∴2Tsindθ=mPQRω2
For small angles sindθ≈dθ
∴2Tdθ=[μ(2R)dθ]Rω2
Solving thr equation, we get
√Tμ=v=Rω
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Level 2 Single Correct
5 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Level 2 More Than One Correct
6 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Level 1 Objective
6 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A loop of rope is whirled at a high angular velocityω, so that it becomes a taut circle of radius r.
(a) Find the tension in the rope it the linear mass density of the rope is μ
(b) A kink develops in the whirling rope. Under what condition does the kink remain stationary relative to an observer on the ground?
View SolutionA horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A.
View SolutionIn the arrangement shown in the fig. a monkey of mass M keeps itself as well as block A at rest by firmly holding the rope. Rope is massless and the pulley is ideal. Height of the monkey and block A from the floor is h and 2h respectively [h = 2.5 m]
(a) The monkey loosens its grip on the rope and slides down to the floor. At what height from the ground is block A at the instant the money hits the ground?
(b) Another block of mass equal to that of A is stuck to the block A and the system is released. The monkey decides to keep itself at height h above the ground and it allows the rope to slide through its hand. With what speed will the block strike the ground?
(c) In the situation described in (b), the monkey decides to prevent the block from striking the floor. The monkey remains at height h till the block crosses it. At the instant the block is crossing the monkey it begins climbing up the rope. Find the minimum acceleration of the monkey relative to the rope, so that the block is not able to hit the floor. Do you think that a monkey can climb with such an acceleration? (g=10ms−2)

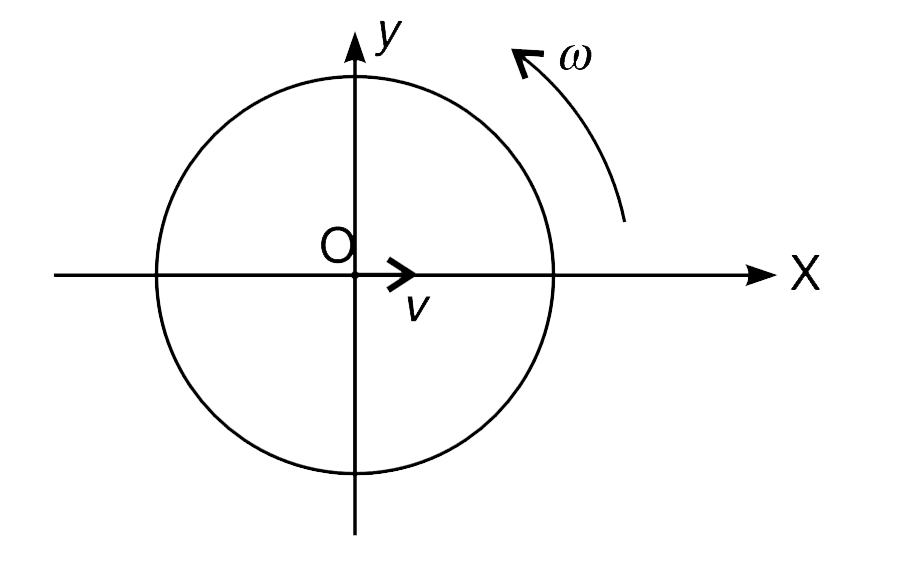
View SolutionA disc is rotating with constant angular velocity ω in anticlockwise direction. An insect sitting at the centre (which is origin of our co-ordinate system) begins to crawl along a radius at time t=0 with a constant speed V relative to the disc. At time t=0 the velocity of the insect is along the X direction.
(a) Write the position vector (→r) of the insect at time ‘t’.
(b) Write the velocity vector (→v) of the insect at time ‘t’.
(c) Show that the X component of the velocity of the insect become zero when the disc has rotated through an angle θ given by tanθ=1θ.
View SolutionFigure shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B.A thick metal rod OA is pivoted at the centre O . The other end of the rod toucher the loop are connected by a wire OC of resistance R.A force is applied at the middle point of the rod OA perpendicularly, so that the rod rotates clockwise at a uniform angular velocity ω . Find the force.
(b) Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its lenght. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠AOC=90∘ .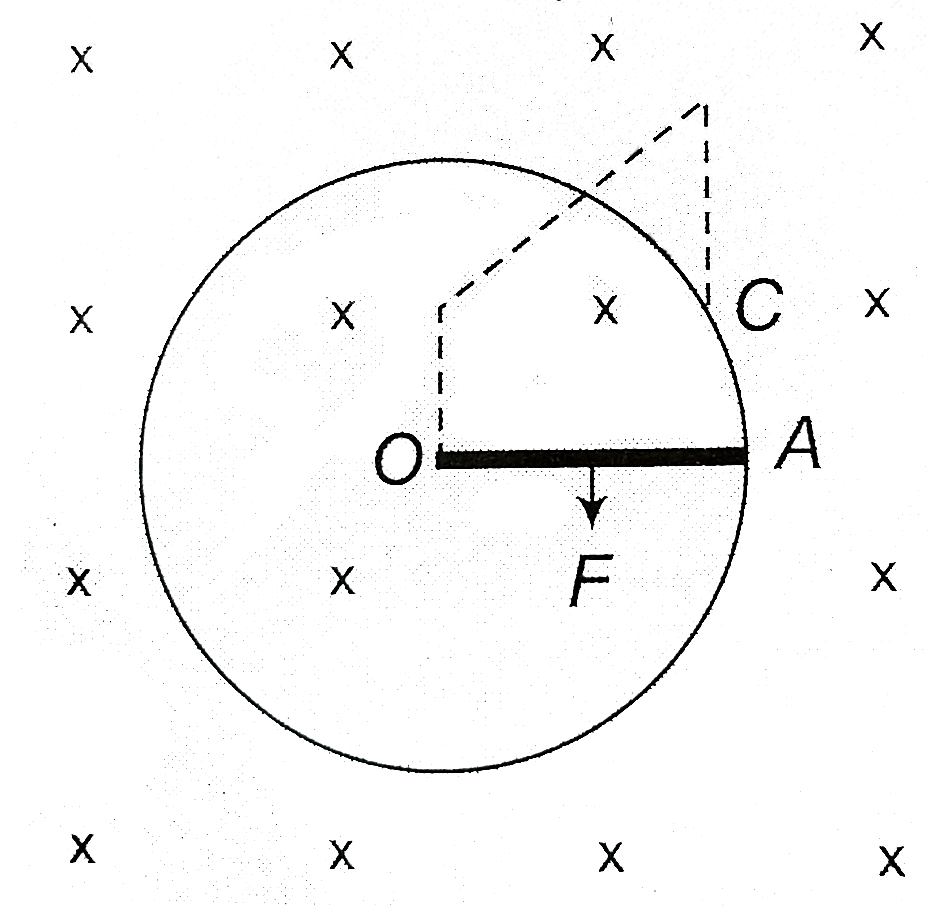
View SolutionA chain (A) of length L is coiled up on the edge of a table. Another identical chain (B) is placed straight on the table as shown. A very small length of both the chains is pushed off the edge and it starts falling under gravity. There is no friction

(a) Find the acceleration of the chain B at the instant L2 length of it is hanging. Assume no kinks in the chain so that the entire chain moves with same speed.
(b) For chain A assume that velocity of each element remains zero until it is jerked into motion with a velocity equal to that of the falling section. Find acceleration of the hanging section at the instant a length l0 has slipped off the table and its speed is known to be v0 at the instant.
View SolutionA horizontal, homogeneous cylinder of mass M and radius R is pivoted about its axis of symmetry. A string is wrapped several times around the cylinder and tied to a body of mass m resting on a support positioned so that the string has no slack. The body of mass m is then lifted vertically to a distance h, and then released.
(a) Evaluate the angular velocity ω0 of the cylinder, the speed v0 of the falling body of mass m, and the kinetic energy K0 of the system, just before the string becomes taut.
(b) Evaluate the corresponding quantities, ω1,v1,andK1, for the instant just after the string becomes taut.
View SolutionA string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
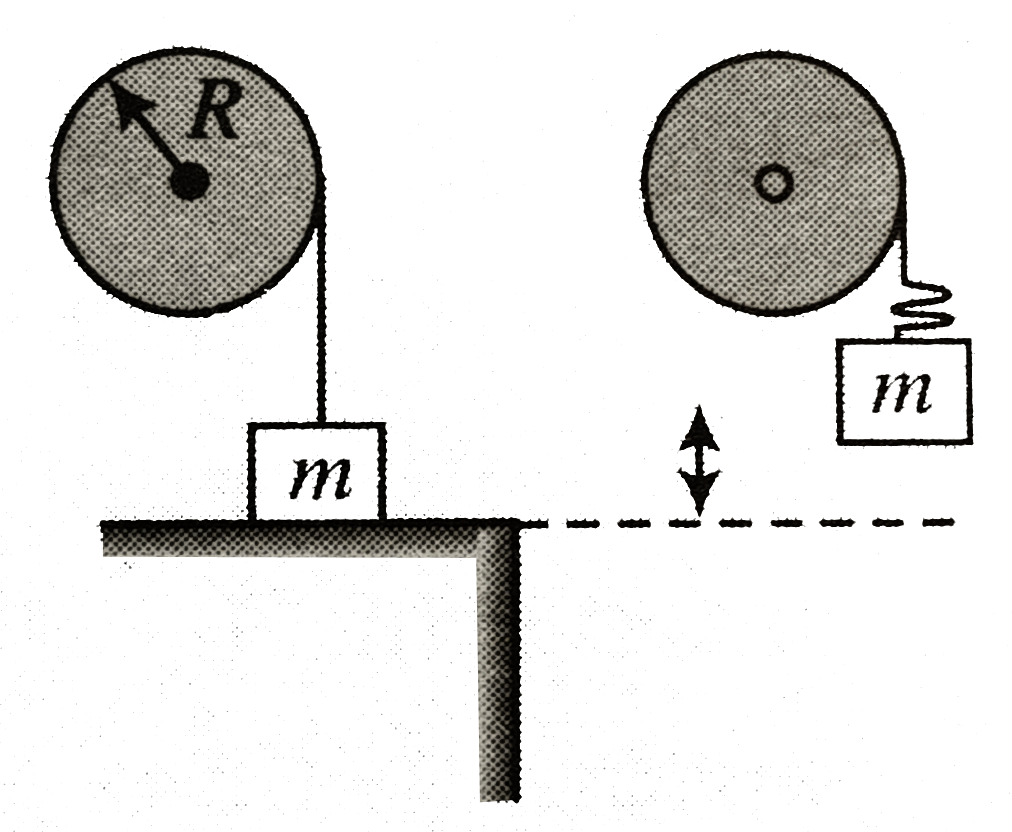
View SolutionA block of mass 25kg rests on a horizontal floor (μ=0.2). It is attached by a 5m long horizontal rope to a peg fixed on floor. The block is pushed along the ground with an initial velocity of 10m/s so that it moves in a circle around the peg. Find
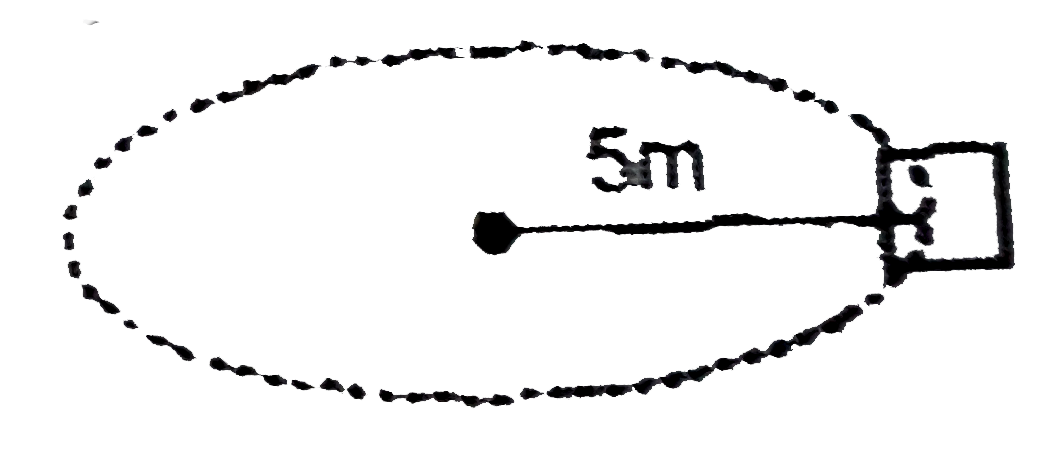
(a) Tangential acceleration of the block.
(b) Speed of the block at time t.
(c) Time when tension in rope becomes zero.
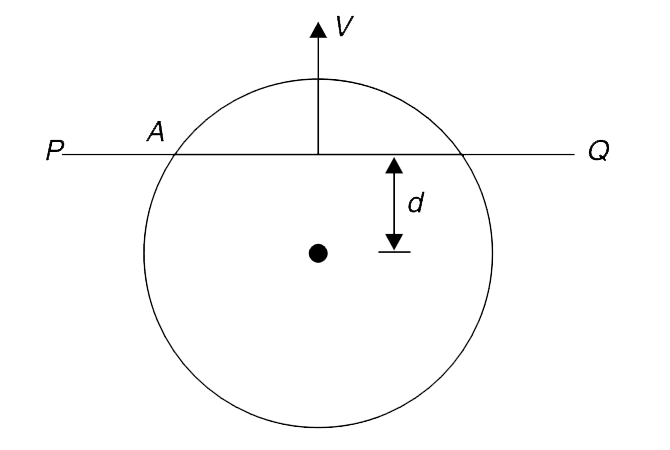
View Solution(a) A line PQ is moving on a fixed circle of radius R. The line has a constant velocity v perpendicular to itself. Find the speed of point of intersection (A) of the line with the circle at the moment the line is at a distance d=R/2 from the centre of the circle.
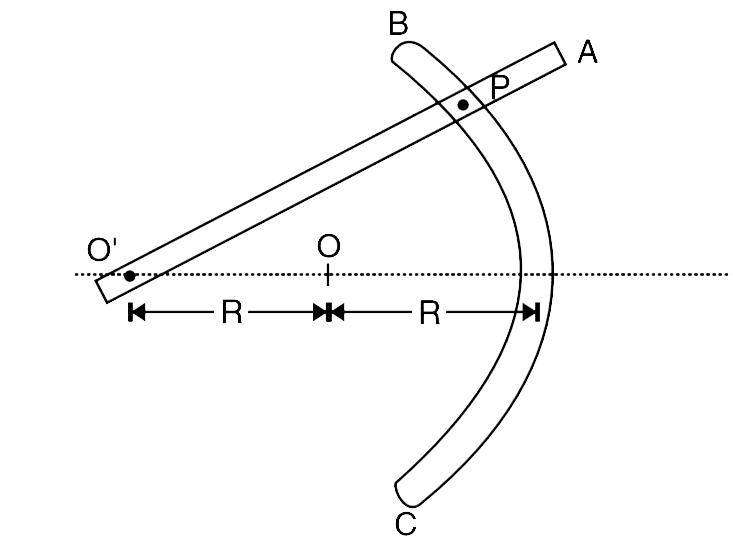
(b) In the figure shown a pin P is confined to move in a fixed circular slot of radius R. The pin is also constrained to remains inside the slot in a straight arm O'A. The arm moves with a constant angular speed w about the hinge O'. What is the acceleration of point P ?
View Solution
