A magentic flux through a statinary loop with a resistance R varies during the tiem interval τ as Φ=at(τ−t). Find the amount of heat generated in the loop during that time. The inductance of the loop is to be neglected.
The amount of heat generated in the loop during a small time interval dl,
dQ=ξ2/Rdt, but ξ=−dΦdt=2at−aτ,
So, dQ=(2at−aτ)2Rdt
and hence, the amoung of heat, generated in the loop during the time interval 0 to τ.
Q=∫τ0(2at−aτ)2Rdt=13a2τ3R
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
The magnetic flux through a stationary loop with a resistanoe R varies during interval of time T as ϕ= at (T−t). If the heat generated during this time, neglecting the inductance of the loop, is a2T3pR, then find p.
View SolutionFind the total heat produced in the loop of the previous problem during the interval 0 to 5s
View Solution
Knowledge Check
- Question 1 - Select One
A magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of the generated in the loop during that time
Aaτ22RBa2τ23RC2a2τ33RDaτ3R - Question 2 - Select One
The magnetic flux through a stationary loop with resistance R varies during interval of time T as ϕ = at (T – t). The heat generated during this time neglecting the inductance of loop will be
Aa2T33RBa2T23RCa2T3RDa2T3R - Question 3 - Select One
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by
AQ=1R.ΔϕΔtBQ=ΔϕRCQ=ΔϕΔtDQ=R.ΔϕΔt
Find the total heat produced in the loop of the previous problem during the interval 0 to 5s
View SolutionFind the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mOmega.
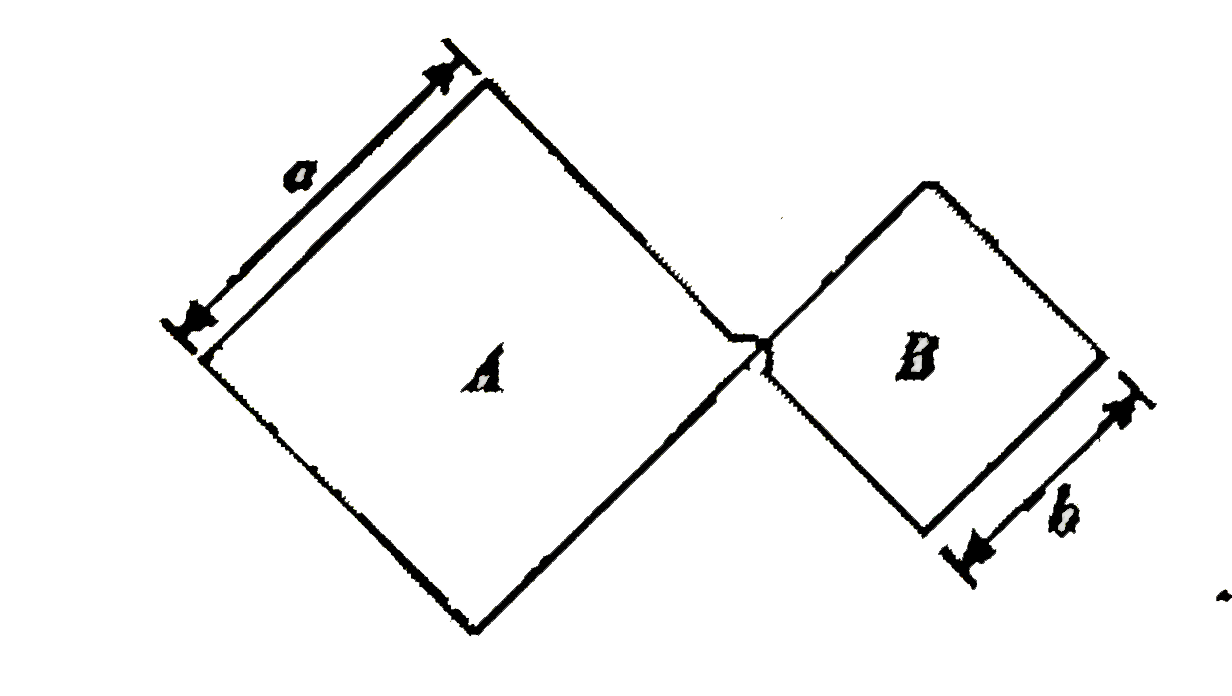
View SolutionA plane loop shown in figure-5.71 is shaped in the from of two squares with sides a and b and it is introduced into a uniform magnetic field at right angles, to the loop's plane. The magnetic induction varies with time as B=B0sinωt. find the amplitude of the current induced in the loop if its resistance per unit length is equal to r. the induction of the loop is negligible.
 View Solution
View SolutionThe electrodes of a capacitor of capacitance C=2.00μF carry opposite charges q0=1.00mC. Then the electores are interconnected through a resistanace R=5.0MΩ. Find:
(a) the charge flowing thorugh that resistance during a time interval τ=2.00s,
(b) the amount of heat generated in the resistance during the same interval.View SolutionThe magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by
View Solution

