A man can swim in still water at a speed of 6 kmph and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of 3 kmph, he has to swim in the direction
30° with the river flow
60° with river flow
135° with the river flow
120° with the river flow
The correct Answer is:D
To solve the problem of the man swimming across the river while accounting for the current, we can break it down into a series of steps:
Step 1: Understand the Problem
The man swims in still water at a speed of 6 km/h, and the river flows at a speed of 3 km/h. He needs to swim in such a way that he reaches a point directly opposite his starting point on the other bank.
Step 2: Set Up the Vectors
We can represent the velocities as vectors:
- Let Vm be the velocity of the man in still water (6 km/h).
- Let Vr be the velocity of the river (3 km/h).
- The resultant velocity Vmr should point directly across the river (from point A to point B).
Step 3: Analyze the Angles
Let θ be the angle between the man's swimming direction and the direction directly across the river. The angle between the man's swimming direction and the river's current will be 90∘+θ.
Step 4: Use Trigonometry
Using the sine rule for the triangle formed by the velocities:
sin(θ)=VrVm
Substituting the values:
sin(θ)=36=12
Step 5: Calculate θ
From the sine function:
θ=sin−1(12)=30∘
Step 6: Determine the Angle α
Since α=90∘+θ:
α=90∘+30∘=120∘
Step 7: Conclusion
The man must swim at an angle of 120∘ with respect to the direction of the river flow to reach the point directly opposite on the other bank.
Final Answer
The angle at which the man has to swim is 120∘ against the river flow.
---
The man swims in still water at a speed of 6 km/h, and the river flows at a speed of 3 km/h. He needs to swim in such a way that he reaches a point directly opposite his starting point on the other bank.
We can represent the velocities as vectors:
- Let Vm be the velocity of the man in still water (6 km/h).
- Let Vr be the velocity of the river (3 km/h).
- The resultant velocity Vmr should point directly across the river (from point A to point B).
Let θ be the angle between the man's swimming direction and the direction directly across the river. The angle between the man's swimming direction and the river's current will be 90∘+θ.
Using the sine rule for the triangle formed by the velocities:
sin(θ)=VrVm
Substituting the values:
sin(θ)=36=12
From the sine function:
θ=sin−1(12)=30∘
Since α=90∘+θ:
α=90∘+30∘=120∘
The man must swim at an angle of 120∘ with respect to the direction of the river flow to reach the point directly opposite on the other bank.
The angle at which the man has to swim is 120∘ against the river flow.
Similar Questions
A man can swim in still water at a speed of 6 kmph and he has to cross the river and reach just opposite point on the other bank. If the river is flowing at a speed of 3 kmph, and the width of the river is 2 km, the time taken to cross the river is (in hours)
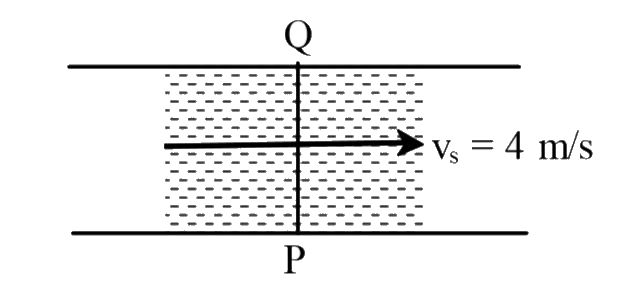
View SolutionA boat man could row his boat with a speed 10 m/sec. He wants to take his boat from P to a point Q just opposite on the other bank of the river flowing at a speed 4 m/sec. He should row his boat–
View SolutionA man can swim in still water at a speed of 4 kmph. He desires to cross a river flowing at a speed of 3 kmph in the shortest time interval. If the width of the river is 3km time taken to cross the river (in hours) and the horizontal distance travelled (in km) are respectively
View SolutionA man can swim in still water ast a speed of 3 km/h. He wants to cross a river that flows at 2 km/h and reach the point directly oposite to his starting point. A. In which diretionshoeld he try to swim (that is, find the angle his body makes wilth the river flow)? b. How much time will he take to cross the river if the river is 500 m wide?
View SolutionA man can swim in still water with a speed of 3m/s x and y axis are drawn along and normal to the bank of river flowing to right with a speed of 1m/s. The man starts swimming from origin O at t = 0 second. Assume size of man to be negligible. Find the equation of locus of all the possible points where man can reach at t = 1 sec

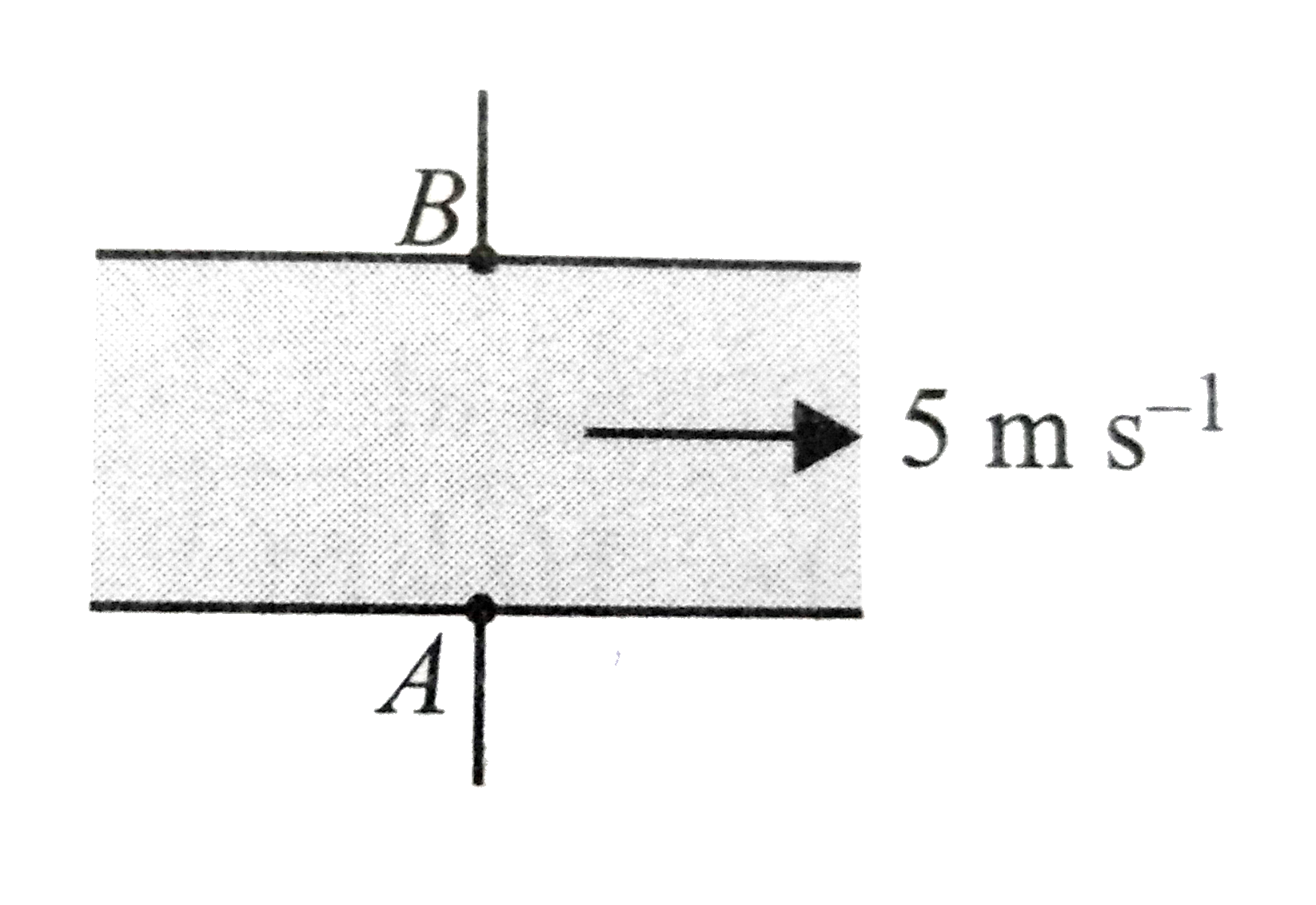
View SolutionA river is flowing from west to east with a speed 5m/s. A swimmer can swim in still water at a speed of 10m/s .
If he wants to start from point A on south bank and reach opposite point B on north bank. In what direction direction should he swim ?
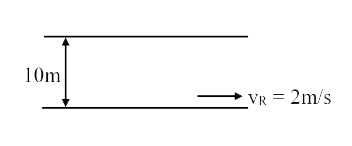
View SolutionA swimmer can swim in still water with a speed of 2.5 m/s. What is the shortest time taken by him to swim across the river?
View SolutionA man can swim in still water with a speed of 2ms−1. If he wants to cross a river of water current speed √3ms−1 along the shortest possible path, then in which direction should he swim ?
View SolutionA man who can swin at the rate of 2 kmhr)(in still river) crosses a river to a point exactly opposite on the other bank by swimming in a direction of 120∘ to the flow of the water in the river. The velocity of the water current in kmhr is
View SolutionA boat can be rowed at 5 m/s on still water. It is used to cross a 200m wide river from the south bank to the north bank. The river current has uniform velocity of 3 m/s due east.
(a) In which direction must it be steered to cross the river perpendicular to current ?
(b) How long will it take to cross the river in a direction perpendicular to the river flow ?
(c) In which direction must the boat be steered to cross the river in minimum time ? How far will it drift ?
View Solution
