A man can swim in still water with a speed v . River flows at a speed u which is greater than the swimming speed (v) of the man . Explain that the man cannot move perpendicular to the flow . If man swims at an angle $θ$ with the river flow , then find drift along the flow by the time he crosses the river . Also find the minimum value of the drift along the flow x by the time he crosses the river .

Video Solution

Text Solution

Verified by Experts

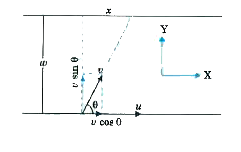
Resultant of v and u will give the net velocity of the man with respect to the ground . Velocity of the man with respect to the ground can be written as follows:
${\to v}_{m} = (u + v cos θ) ˆ i + (u sin θ) ˆ j$
Time taken to cross the river can be calculated using Y-component of velocity .
$t = \frac{w}{v sin θ}$
Drift in this time interval can be calculated using X-component of velocity .
$x = (u + v cos θ) t$
Substituting from equation (i) we get the following:
$x = (u + v cos θ) (\frac{w}{v sin θ}) \Rightarrow x = w \frac{u + v cos θ}{u sin θ}$
We can use differentation to calculate the minimum value of x , but for now let us make use of quadratic equation. On squaring and rearranging the equation (ii) , we get the following :
$v^{2} x^{2} {sin}^{2} θ = w^{2} u^{2} {cos}^{2} θ + 2 u u w^{2} cos θ$
$\Rightarrow v^{2} x^{2} (1 - {cos}^{2} θ) = w^{2} u^{2} + w^{2} v^{2} {cos}^{2} θ + 2 u u w^{2} cos θ$
$\Rightarrow (w^{2} v^{2} + v^{2} x^{2}) {cos}^{2} θ + 2 u u w^{2} cos θ + (w^{2} u^{2} - v^{2} x^{2}) = 0$
For real solution of $cos, θ$ , discriminate of the above equation must be greater than zero . Hence we can write the following :
$Δ \geq 0$
$B^{2} - 4 A C \geq 0$
$\Rightarrow 4 u^{2} v^{2} w^{2} - 4 (w^{2} v^{2} + v^{2} x^{2}) (w^{2} u^{2} - v^{2} x^{2}) \geq 0$
$\Rightarrow u^{2} w^{2} - (w^{2} + x^{2}) (w^{2} u^{2} - v^{2} x^{2}) \geq 0$
$\Rightarrow u^{2} w^{2} - w^{2} u^{2} - x^{2} w^{2} u^{2} + w^{2} v^{2} x^{2} + v^{2} x^{4} \geq 0$
$\Rightarrow - x^{2} w^{2} u^{2} + w^{2} v^{2} u^{2} + w^{2} v^{2} x^{2} + v^{2} x^{4} \geq 0$
$\Rightarrow v^{2} x^{2} \geq w^{2} (u^{2} - v^{2})$
$\Rightarrow x^{2} \geq \frac{w^{2}}{v^{2}} (u^{2} - v^{2})$
$\Rightarrow x \geq \frac{w}{v} \sqrt{(u^{2} - v^{2})}$
From the above result we can write the maximum value of x.
$\Rightarrow x_{min} = \frac{w}{v} \sqrt{(u^{2} - v^{2})}$

Updated on:21/07/2023