A man can swim in still water with speed v. He wants to cross a river of width d that flows with speed u and reaches the point directely opposite to his starting point. (a) In which direction should he try to swim (i.e., find the angle the makes with the river flow)? (b) much time will he take to cross the river ?
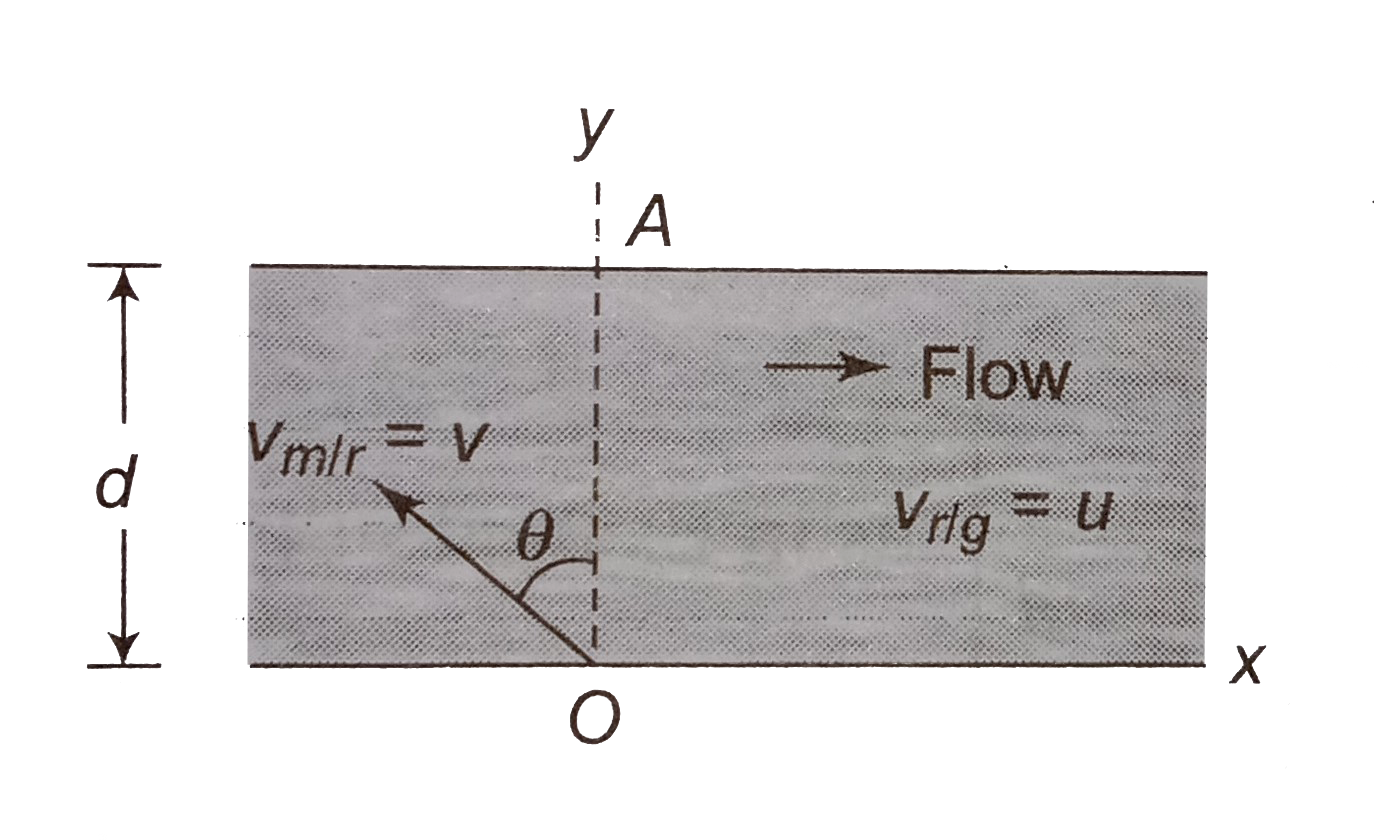
O: straight point
A: Destination point
To reach to point A, the man should swim at an angle θ with OA as shown.
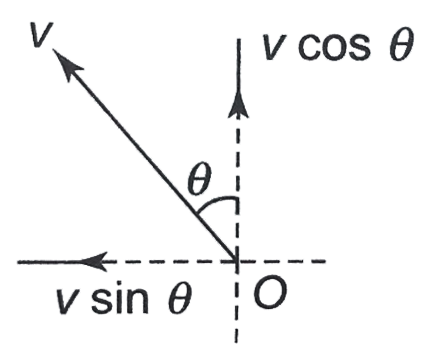
(vm/g)x=vsinθ−u
(vm/g)y=vcosθ
x: (uniform motion),displacement =0
x=(vsinθ−u)t=0
⇒vsinθ=u
sinθ=uv⇒θ=sin−1(uv)
y: (uniform motion), displacement =d
t=dvcosθ=dv√1−sin2θ=dv√1−u2v2=d√v2−u2
Topper's Solved these Questions
Similar Questions
A man can swim in still water ast a speed of 3 km/h. He wants to cross a river that flows at 2 km/h and reach the point directly oposite to his starting point. A. In which diretionshoeld he try to swim (that is, find the angle his body makes wilth the river flow)? b. How much time will he take to cross the river if the river is 500 m wide?
View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?
View Solution
Knowledge Check
A man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
AThe minimum time in which he can cross the river is bvBHe can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>uCHe cannot reach a point exactly opposite on the bank if u>vDHe cannot reach a point exactly opposite on the bank if v>uA man who can swim at a speed v relative to the water wants to cross a river of width d, flowing with a speed u. The point opposite him across the river is P.
AThe minimum time in which he can cross the river is dvBHe can reach the point P in time dvCHe can reach the point P in time d√v2−u2DHe cannot reach P if u>vA man who can swim at a speed v relative to the water wants to cross a river of width d flowing with a speed u. The point opposite him across the river is A.
AHe can reach the point A in time d/vBHe can reach the point A is time d√v2−u2CThe minimum time in which he can cross river is dvDHe can not reach A if u gt v
A man can row a boat at 4.0km/hr in still water. A river flows at 2.0km/hr. (a) if he is crossing the river, in what direction the oat shou ld go to reach a point directly opposite to his staring point? (b) if the river is 4.0km wide how long will it take him to cross the river? (c) How long will it take him to row 2.0km down the river and then back to his starting point? (d) How long will it take him to row 2.0 km up the river and then back to his starting point? (e) in what direction the boat shou ld go, if he wants to cross he river in teh smallest possible time?
View SolutionA boat can swim in still water with speed of 20 km/h . a river of width 500 meters flows with speed of 6 km./h. In what direction . . . . should the boat be pointed , so that it reaches the opposite bank at the point directly opposite the starting point ? Also find the time . . . . . taken. Is this the least time of crossing ?
View SolutionA man can swim in still water with a speed v . River flows at a speed u which is greater than the swimming speed (v) of the man . Explain that the man cannot move perpendicular to the flow . If man swims at an angle θ with the river flow , then find drift along the flow by the time he crosses the river . Also find the minimum value of the drift along the flow x by the time he crosses the river .
View SolutionA man can swim in still water with a speed of 2ms−1. If he wants to cross a river of water current speed √3ms−1 along the shortest possible path, then in which direction should he swim ?
View SolutionA man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
View Solution
