A man is walking due west with a velocity $3 k m / h$ and rain appears to be falling vertically with a velocity $4 k m / h$ . Find the velocity of rain with respect to the ground.

Video Solution

Text Solution

Verified by Experts

Here, $4 k m / h$ is the velocity of rain with respect to the man.
$v_{r / m} = 4 k m / h$ , vertically downward
$v_{m / g} = 3 k m / h$ towards west
$v_{r / g} = ?$
Since $v_{r / m}$ is resultant of $v_{r / g}$ and $v_{m / g}$ (in opposite direction)

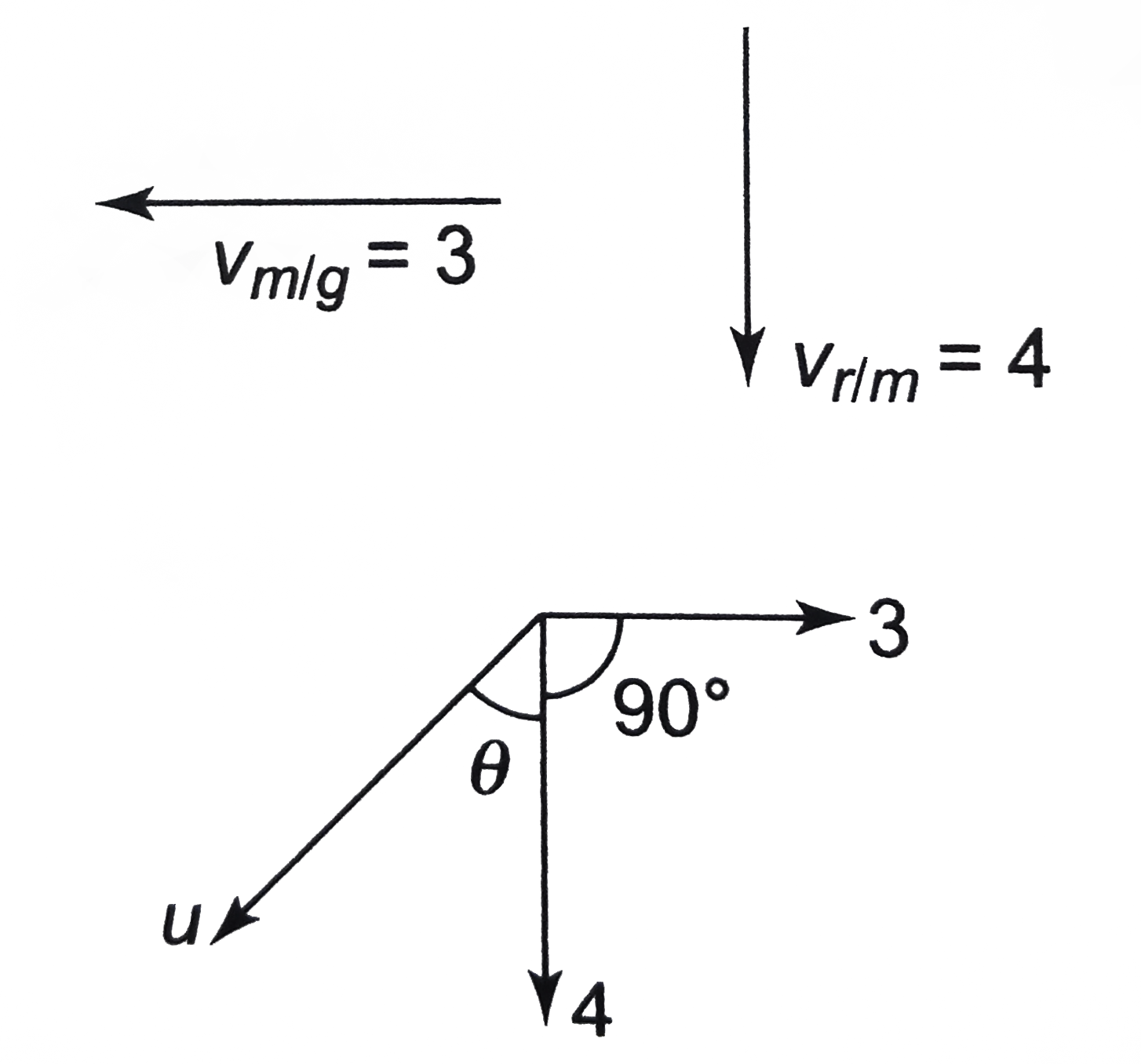
$u : v_{r / g}$ (actual velocity of rain)
${\tan 90}^{\circ} = \frac{u \sin (90 + θ)}{3 + u \cos (90 + θ)}$
$\frac{1}{0} = \frac{u \cos θ}{3 - u \sin θ} \Rightarrow u \sin θ = 3 ... ... . (i)$
$[\cos (90 + θ) = - \sin θ]$
${(v_{r / m})}^{2} = {(v_{m / g})}^{2} + {(v_{r / g})}^{2} + 2 (v_{m / g}) (v_{r / g}) \cos (90 + θ)$
${(4)}^{2} = {(3)}^{2} + u^{2} + 2 (3) (u) (- \sin θ)$
$16 = 9 + u^{2} - 2 \times 3 \times 3 \Rightarrow u^{2} = 25 \Rightarrow \cup = 5 k m / h$
$u \sin θ = 3 \Rightarrow 5 \sin θ = 3 \Rightarrow \sin θ = \frac{3}{5} \Rightarrow θ = 37^{\circ}$
Rain is falling with a speed of $5 k m / h$ at an angle $37^{\circ}$ with vertical.
OR
Component approach

$u \sin θ - 3 = 0 \Rightarrow u \sin θ = 3$
$u \cos θ = 4$
$u = \sqrt{{(u \sin θ)}^{2} + {(u \cos θ)}^{2}} = 5 k m / h$
$\tan θ = \frac{u \sin θ}{u \cos θ} = \frac{3}{4} \Rightarrow θ = 37^{\circ}$
OR
${\vec{v}}_{r / m} = - 4 \hat{k}, {\vec{v}}_{m / g} = - 3 \hat{j}$
${\vec{v}}_{r / m} = {\vec{v}}_{r / g} - {\vec{v}}_{m / g}$
$= - 4 \hat{k} = {\vec{v}}_{r / g} - (- 3 \hat{j})$
${\vec{v}}_{r / g} = - 3 \hat{j} - 4 \hat{k}$
$| {\vec{v}}_{r / g} | = v_{r / g} = \sqrt{{(- 3)}^{2} + {(- 4)}^{2}} = 5 k m / h$
$\tan θ = \frac{3}{4} \Rightarrow 37^{\circ}$

Updated on:21/07/2023

A man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
A7 km/hr
B5 km/hr
C4/3 km/hr
D3/4 km/hr
Rain is falling vertically downward with velocity $4 m / s .$ A man is moving horizontally with velocity $3 m / s$ , the velocity of rain with respect to man is
A $5 m / s$ at an angle ${tan}^{- 1} (4 / 3)$ with horizontal
B $5 m / s$ at an angle ${tan}^{- 1} (3 / 4)$ with vertical
C $5 m / s$ at an angle ${tan}^{- 1} (4 / 3)$ with vertical
DBoth $(1)$ and $(2)$