A man of mass m having a bag ofmas m slips from the roof of atall building of height H and starts falling vertically figure. When at a height h from the ground, he notices that the ground below him is pretty hard but there is a pond at a horizontal distnce x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just suceeds toavoid the hard ground, where will the bag land?
 Solution in Tamil
Solution in Tamil
Mass of man =M,
Initial velocity =O Mass of bag = m
Let the man throws the bag towards left with a velocity v.
So there is no exterN/Al force in the horizontal direction
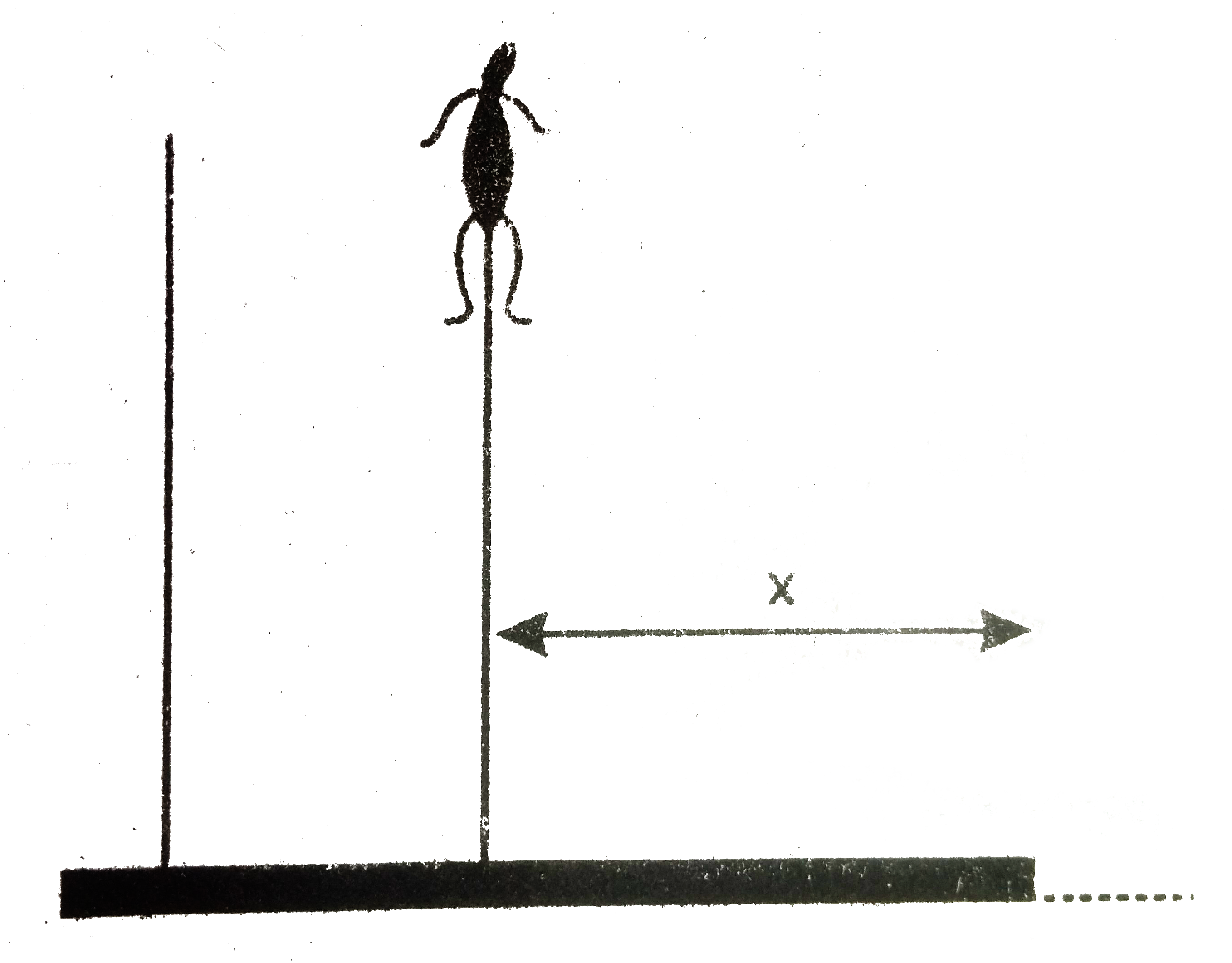
The momentum will be conserved.
Let the goes right with a velocity
mv=MV
rarr V=((mv)/M)<br>rarr v=((MV)/m)............i<br>Letthe→taltimehewilltake→reachgrond<br>=sqrt((2H)/g)=t_1<br>Letthe→taltimehewilltake→reachtheheighth<br>=t_2=sqrt((2(H-h))/g)<br>Thenthetimeofhisfly∈g<br>=t_1-t_2<br>=((2h)/g-)sqrt((2(H-h))/g)<br>=sqrt(2/g)(sqrtH-sqrt(H-h)<br>with∈thistimehereachestheground∈thepondcover∈gahorizontaldistance<br>rarr x=Vxxt <br>rarr V=x/t<br>v=M/m x/t<br>=M/mxxxx sqrtg/(sqrt(2)(sqrtH-sqrt(H-h))x<br>AsthereisnoexterNAlforce∈horizontaldirectionthex−corrdiNAteofCMwillrema∈attˆposition.<br>rarr 0=(Mxx(x)+mxxx_1)/(M+m)<br>rarr x_1=M/mx<br>:.Thebagwillreachthe⊥→matadistance(M/m)x towards left of the line it falls.
Topper's Solved these Questions
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
01:28View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
01:22View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
04:43View SolutionA ball of mass m falls vertically to the ground from a height h1 and rebound to a height h1 and rebound to a height h2. The change in momentum of the ball on striking the ground is.
01:50View SolutionA boy playing on the roof of a 10m high building throws a ball with a speed of 10m/s at an angle of 30(∘) with the horizontal. How far from the throwing point will the ball be at the height of 10m from the ground ?
[g=10m/s2,sin30∘=12,cos30∘=√32]12:35View SolutionStatement-1 : A man falling from a given height on hard ground is hurt more than falling on a soft bed from same height.
Statement-2 : A man falling from a given height on hard ground experiences larger impulse than falling on a soft bed in coming to rest in both cases.04:06View SolutionA man goes 80 m on an inclined cliff inclined at 45∘ from the horizontal. Find the vertical height of the man from the ground.
02:35View SolutionM द्रव्यमान का एक मनुष्य जिसके हाथ में m द्रव्यमान का एक बैग है, एक ऊँची इमारत के छज्जे से फिसल जाता है और ऊर्ध्वाधर दिशा में गिरने लगता है इमारत की ऊँचाई H है | जब वह जमीन से h दूरी पर है , तब वह देखता है कि नीचे कि जमीन बहुत कठोर है, परंतु उससे क्षैतिज दूरी x पर एक तालाब है | अपने को कठोर जमीन पर गिरने से बचाने के लिए मनुष्य अपने बैग को, अपनी अपेक्षा क्षैतिज दिशा में, तालाब से विपरीत दिशा में फेकता है| वह बैग को न्यूनतम कितना क्षैतिज वेग दे ताकि वह (मनुष्य) पानी में गिरे | यदि वह पानी में बिलकुल कठोर जमीन के पास में ही गिरता है तो बैग जमीन पर कहाँ गिरेगा ?
 07:48View Solution
07:48View SolutionA man in a moving bus drops a bag from a height 2 m. The bag lands on the ground with a velocity 10 m/s. The velocity of the bus at the moment he dropped the bag was:
05:34View SolutionTwo bodies of masses m _(1) and m _(2) fall from heights h _(1) and h _(2) respectively. The ratio of their velocities when the hit the ground is
02:56View SolutionA ball is thrown vertically upwards from the ground at a height of h at a speed of v. When will the ball fall to the ground again?
View SolutionTwo objects of masses m1andm2 fall from the heights h1andh2 respectively. The ratio of the magntidue of their momenta when they hit the ground is
03:05View SolutionAn aircraft is moving in a horizontal direction at a height of 1960 m from the ground at a speed of 600 km / h. When it is directly above the point A of the ground, then it drops an object. This object falls on the point B on the ground, then the value of AB is
View SolutionFrom the top of a building of height h, a tower standing on the ground is observed to make an angle θ. If the horizontal distance between the building and the tower is h, the height of the tower is
03:43View Solutionएक पिण्ड को h ऊँचाई की मीनार से √2gh वेग के साथ क्षैतिज दिशा में फेंका जाता है। वह मीनार के तल से x दूरी पर जमीन पर गिरता है। x का मान है :-
02:34View SolutionA man (m1) with a bag (m2) in hand falls freely vertically from a height h above the ground. After falling through a height y0, man throws bag horizontally with a velocity u0 towards his right.
03:05View Solution
