A man slowly pulls a bucket of water from a well of depth h=20m. The mass of the uniform rope and bucket full of water are m=200g and M 19.9kg, respectively. Find the work done (∈kJ) by the mean.
The correct Answer is:(4)
To find the work done by the man in pulling the bucket of water from the well, we can use the concept of gravitational potential energy. The work done is equal to the change in potential energy of both the bucket and the rope as they are lifted.
1. Identify the masses and height:
- Mass of the bucket (full of water), M=19.9kg
- Mass of the rope, m=200g=0.2kg (convert grams to kilograms)
- Depth of the well, h=20m
2. Calculate the change in potential energy for the bucket:
- The potential energy change for the bucket when it is lifted from a depth of 20 m to the top is given by:
ΔPEbucket=M⋅g⋅h
- Where g≈9.81m/s2 (acceleration due to gravity).
- Substituting the values:
ΔPEbucket=19.9kg⋅9.81m/s2⋅20m
3. Calculate the change in potential energy for the rope:
- The rope is uniform, and its center of mass is at half its length when fully extended. Therefore, the center of mass of the rope is at a height of 202=10m.
- The potential energy change for the rope is given by:
ΔPErope=m⋅g⋅hcm
- Where hcm=10m (height of the center of mass of the rope).
- Substituting the values:
ΔPErope=0.2kg⋅9.81m/s2⋅10m
4. Calculate the total work done:
- The total work done by the man is the sum of the work done to lift the bucket and the rope:
W=ΔPEbucket+ΔPErope
5. Perform the calculations:
- For the bucket:
ΔPEbucket=19.9⋅9.81⋅20=3900.78J
- For the rope:
ΔPErope=0.2⋅9.81⋅10=19.62J
- Total work done:
W=3900.78+19.62=3920.4J
6. Convert the work done to kilojoules:
W=3920.41000=3.9204kJ
Final Answer:
The work done by the man is approximately 3.92kJ.
- Mass of the bucket (full of water), M=19.9kg
- Mass of the rope, m=200g=0.2kg (convert grams to kilograms)
- Depth of the well, h=20m
- The potential energy change for the bucket when it is lifted from a depth of 20 m to the top is given by:
ΔPEbucket=M⋅g⋅h
- Where g≈9.81m/s2 (acceleration due to gravity).
- Substituting the values:
ΔPEbucket=19.9kg⋅9.81m/s2⋅20m
- The rope is uniform, and its center of mass is at half its length when fully extended. Therefore, the center of mass of the rope is at a height of 202=10m.
- The potential energy change for the rope is given by:
ΔPErope=m⋅g⋅hcm
- Where hcm=10m (height of the center of mass of the rope).
- Substituting the values:
ΔPErope=0.2kg⋅9.81m/s2⋅10m
- The total work done by the man is the sum of the work done to lift the bucket and the rope:
W=ΔPEbucket+ΔPErope
- For the bucket:
ΔPEbucket=19.9⋅9.81⋅20=3900.78J
- For the rope:
ΔPErope=0.2⋅9.81⋅10=19.62J
- Total work done:
W=3900.78+19.62=3920.4J
W=3920.41000=3.9204kJ
The work done by the man is approximately 3.92kJ.
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (sinble Correct )
Explore 19 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives(multiple Correct)
Explore 3 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A man pulls a bucket of water from a depth of h from a well. If the mass of the rope and that of bucket full of water are m and M respectively, the work done by the man is :
View SolutionA person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
View SolutionA bucket tied to a string is lowered at a constant acceleration of g/4. If mass of the bucket is m and it is lowered by a distance l then find the work done by the string on the bucket.
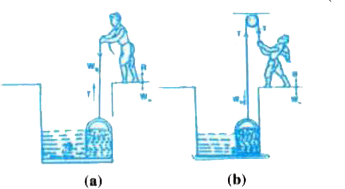
View SolutionA man wants to draw a bucket full of water in two different ways. As shown in figure 'a' he draws the bucket directly and as shown in figure (b) he uses a pulley. The weight of the man is 50kg and the bucket with full water weighs 25kg. Find the action on the floor by the man in the two cases. (Take g=10ms−2).
View SolutionA body of mass m was slowly pulled up the hill by a force F which at each point was directed along the tangent of the trajectory. All surfaces are smooth. Find the work done by this force

View SolutionA bucket full of water weighs 5 kg, it is pulled from a well 20 m deep. There is a small hole in the bucket through which water leaks at a constant rate. If it is observed that for every meter the bucket loses 0.2 kg mass of water, then the total work done in pulling the bucket up from the well is [g=10ms−2]
View SolutionA uniform chain of length 4m is kept on a table such that a length of 120 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg What is the work done in pulling the entire chain on the table ?
View SolutionA man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g2 then the work done by the string on the block will be
View SolutionThe sign of work done by a force is important to understant. State carefully if the following quantities are positive or negative. (a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket. (b) Work done by the gravitational force in the above case. (c ) Work done by friction on a body sliding down an inclined plane. (d) Work done by an applied froce on a body moving on a rough horizontal plane with uniform velocity. (e ) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
View SolutionA woman draws water from a well using a fixed pulley. The mass of bucket and water together is 6 kg. the force applied by the woman is 70 N. calculate the mechanical advantage. (Take g=10ms−2)
View Solution
