A man walking briskly in rain with speed v must slant his umbrella forward making an angle θ with the vertical. A student derives the following relation between θ and v as tan θ=v and checks that the relation has a correct limit when v→0,θ→0 as expected. Do you think the relation can be correct? If not guess out the correct relation.
The correct Answer is:tanθ must be dimensionless. The correct formula is tanθ=v/u where u is the initial velocity of the rain.
To solve the problem, we need to analyze the relationship between the angle θ that the umbrella makes with the vertical and the speed v of the man walking in the rain. The initial claim is that tanθ=v, but we need to check if this is dimensionally correct and if it makes sense in the context of the problem.
1. Understanding the Scenario:
- A man is walking in the rain with speed v.
- He tilts his umbrella at an angle θ with respect to the vertical to avoid getting wet.
2. Analyzing the Forces:
- The rain is falling vertically with some speed vr.
- The man is moving horizontally with speed v.
- The resultant velocity of the rain relative to the man will be a combination of these two velocities.
3. Finding the Resultant Velocity:
- The horizontal component of the rain's velocity is v (the man's speed).
- The vertical component of the rain's velocity is vr (the speed of rain falling).
- The angle θ can be defined using the tangent function:
tanθ=oppositeadjacent=vvr
4. Checking the Given Relation:
- The student derived the relation tanθ=v.
- This is dimensionally incorrect because tanθ is dimensionless (it has no units), while v has dimensions of (L)(T−1).
- Therefore, the relation tanθ=v cannot be correct.
5. Finding the Correct Relation:
- From our analysis, we found that the correct relation should be:
tanθ=vvr
- This indicates that the angle θ depends on the ratio of the man's speed to the speed of the rain.
6. Limit Check:
- As v→0 (the man is standing still), we expect θ→0 if vr is non-zero.
- This limit holds true for the derived relation tanθ=vvr.
Conclusion:
The relation tanθ=v is incorrect. The correct relation is:
tanθ=vvr
- A man is walking in the rain with speed v.
- He tilts his umbrella at an angle θ with respect to the vertical to avoid getting wet.
- The rain is falling vertically with some speed vr.
- The man is moving horizontally with speed v.
- The resultant velocity of the rain relative to the man will be a combination of these two velocities.
- The horizontal component of the rain's velocity is v (the man's speed).
- The vertical component of the rain's velocity is vr (the speed of rain falling).
- The angle θ can be defined using the tangent function:
tanθ=oppositeadjacent=vvr
- The student derived the relation tanθ=v.
- This is dimensionally incorrect because tanθ is dimensionless (it has no units), while v has dimensions of (L)(T−1).
- Therefore, the relation tanθ=v cannot be correct.
- From our analysis, we found that the correct relation should be:
tanθ=vvr
- This indicates that the angle θ depends on the ratio of the man's speed to the speed of the rain.
- As v→0 (the man is standing still), we expect θ→0 if vr is non-zero.
- This limit holds true for the derived relation tanθ=vvr.
The relation tanθ=v is incorrect. The correct relation is:
tanθ=vvr
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM DERIVATION OF FORMULAE USING DIMENSIONS)5videos
DIMENSIONS
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
Similar Questions
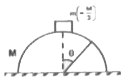
A smooth hemisphere of mass M is kept on a smooth surface. A block of mass m(=M/3) is kept on the top of the hemisphere as shown in the figure. The hemisphere is displaced slightly ang both the hemisphere and the block starts moving. At an angle θ with the vertical ( subtended by the block at the centre of the hemisphere ) , the relation between the velocity of the block ( V) and the velocity of the hemishere ( v0 ) is (V is the velocity of the block w.r.t. the hemisphere at that instant . )
 View Solution
View SolutionA circular railway track of radius r is banked at angle θ so that a train moving with speed v can safely go round the track. A student writes: tanθ=rg/v2. Why this relation is not correct?
(i) Equality of dimensions does not guarantee correctness of the relation .
(ii) Dimensionally correct relation may not be numerically correct.
iii) The relation is dimensionally incorrect.View SolutionSuppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cosθ=1−θ22andsinθ=θ for small theta.
View SolutionA child is swinging a ball of mass M around on a light spring which has spring constant k. The ball describes a horizontal circle. The stretched spring has a length a horizontal circle. The stretched spring has a length l and makes an angle θ with the vertical as shown in fig. the acceleration due to gravity is g neglect air resistance.
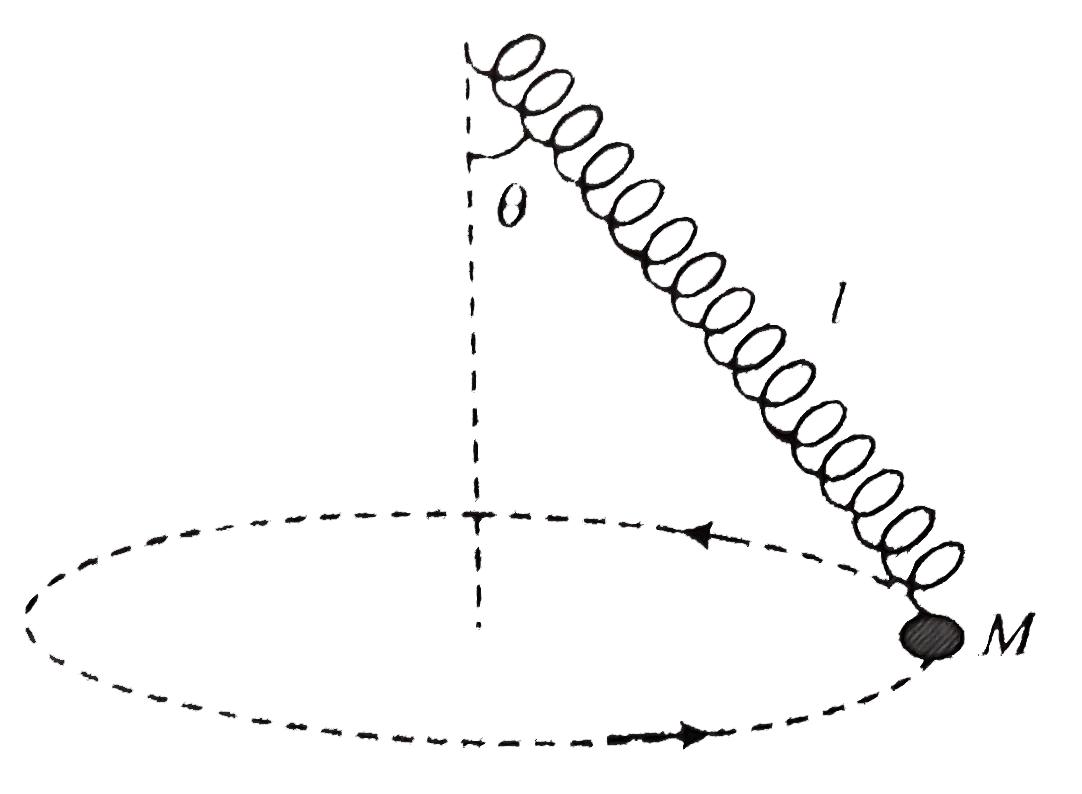
a. In terms of only the given quantities , what is the magnitude of force F that the spring exerts on man M?
b.In terms of F,kand lwhat is the natural length l0 of the spring i.e. the length of the spring when it is not steched?
c. In terms of F,l,M and B what is the speed v of the ball?View SolutionConsider the motion of a positive point charge in a region where there are simultaneous uniform eletric and magnetic field E=E0ˆj and B=B0ˆj. At time t=0, this charge has velocity v in the x-y-plane making an angle θ with the x-axis. Which of the following option(s) is (are) correct for time t>0?
a. If θ=00 the charge moves in a circular path in the xy-plane.
b.Ifθ=00 the charge undergoes helical motion with constant pitch along the y-axis.
c. If θ=100 the charge undergoes helicalmotion with its pitch increasing with time along the y-axis.
d. If θ=90∘ the charge undergoes linear but accelerated motion along the y-axis.View Solution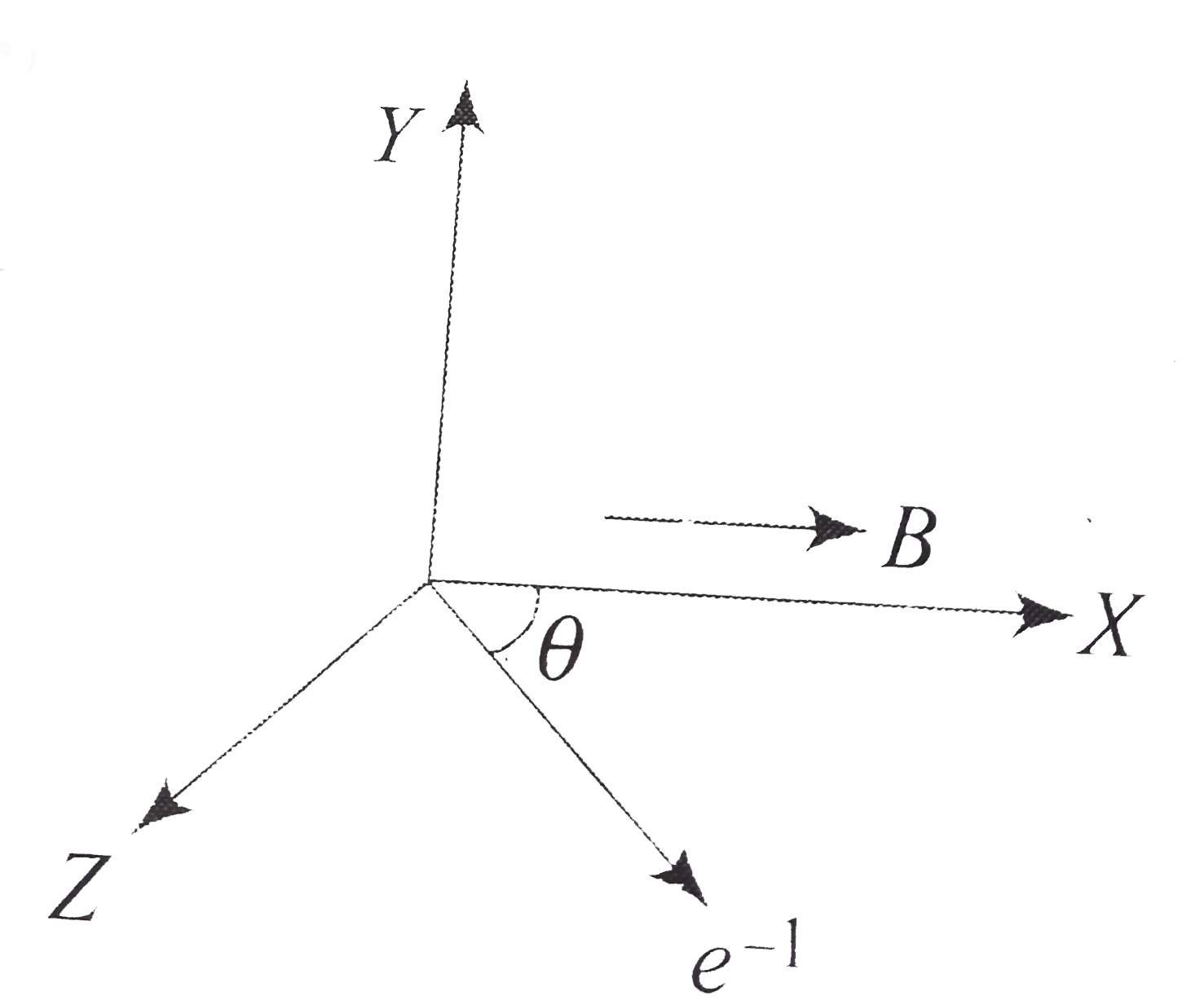
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
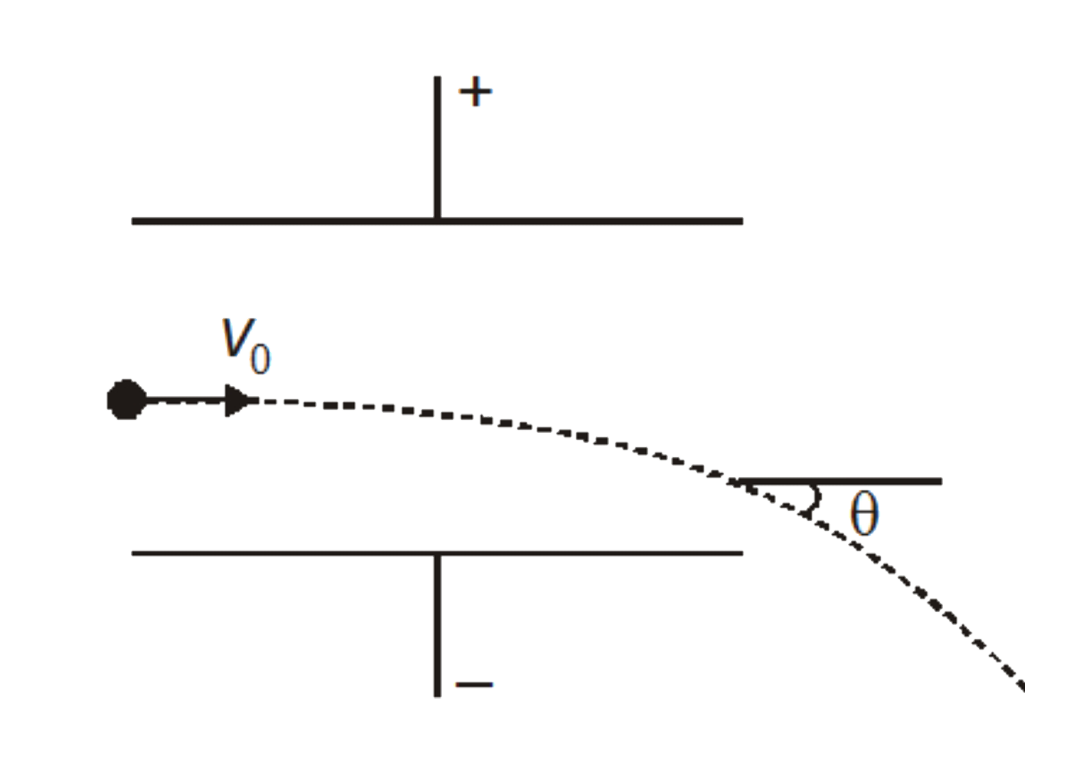
Q. The correct relation between p and B0 isView Solutionwhen a positively charged particle is projected with a velocity v0 in the region between the horizontal plates of the capacitor then it leaves by making an angle θ with the horizontal , as shown. If θ=θ1 is for proton and θ=θ2 for an α - particle then the value of tanθ1tanθ2
 View Solution
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.
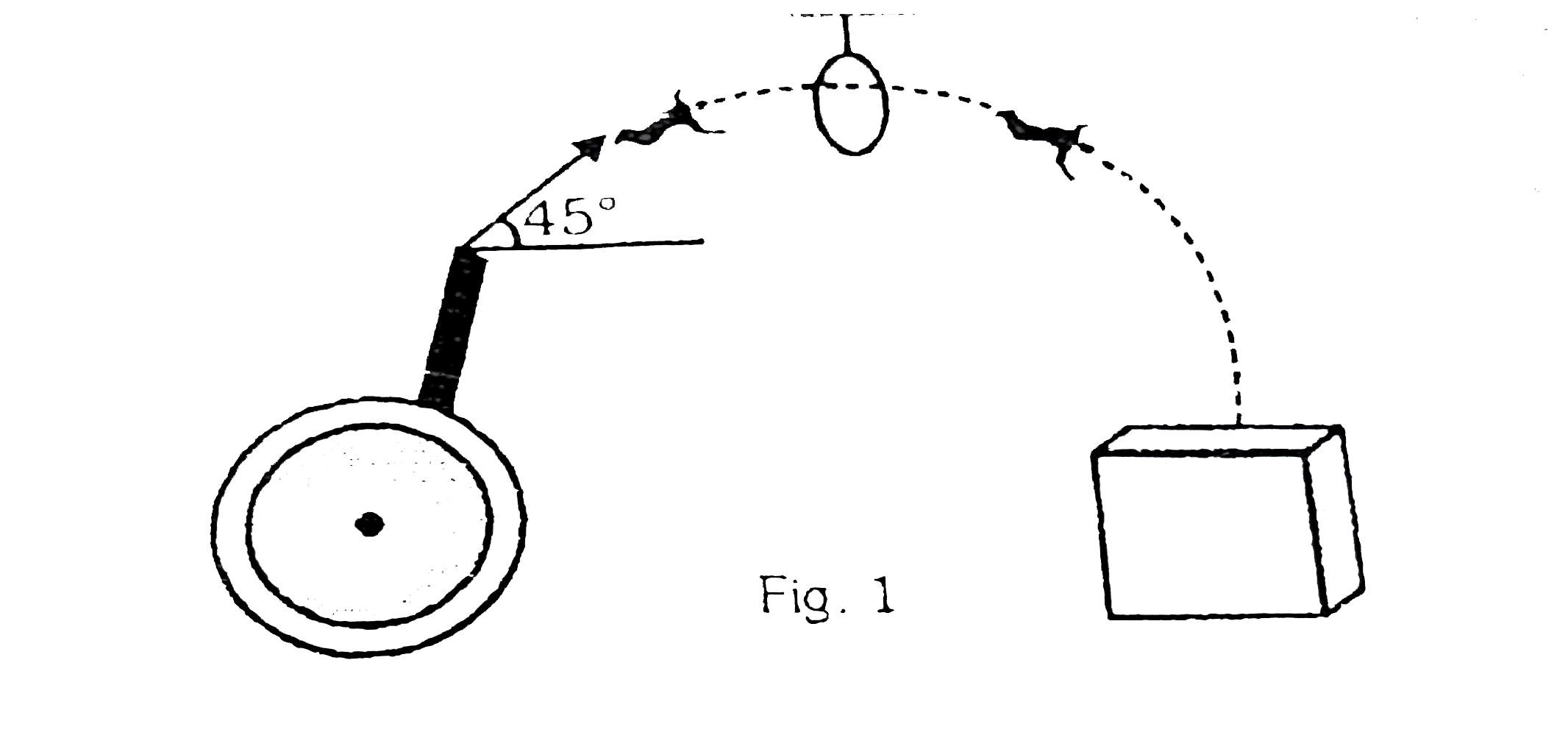
A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.
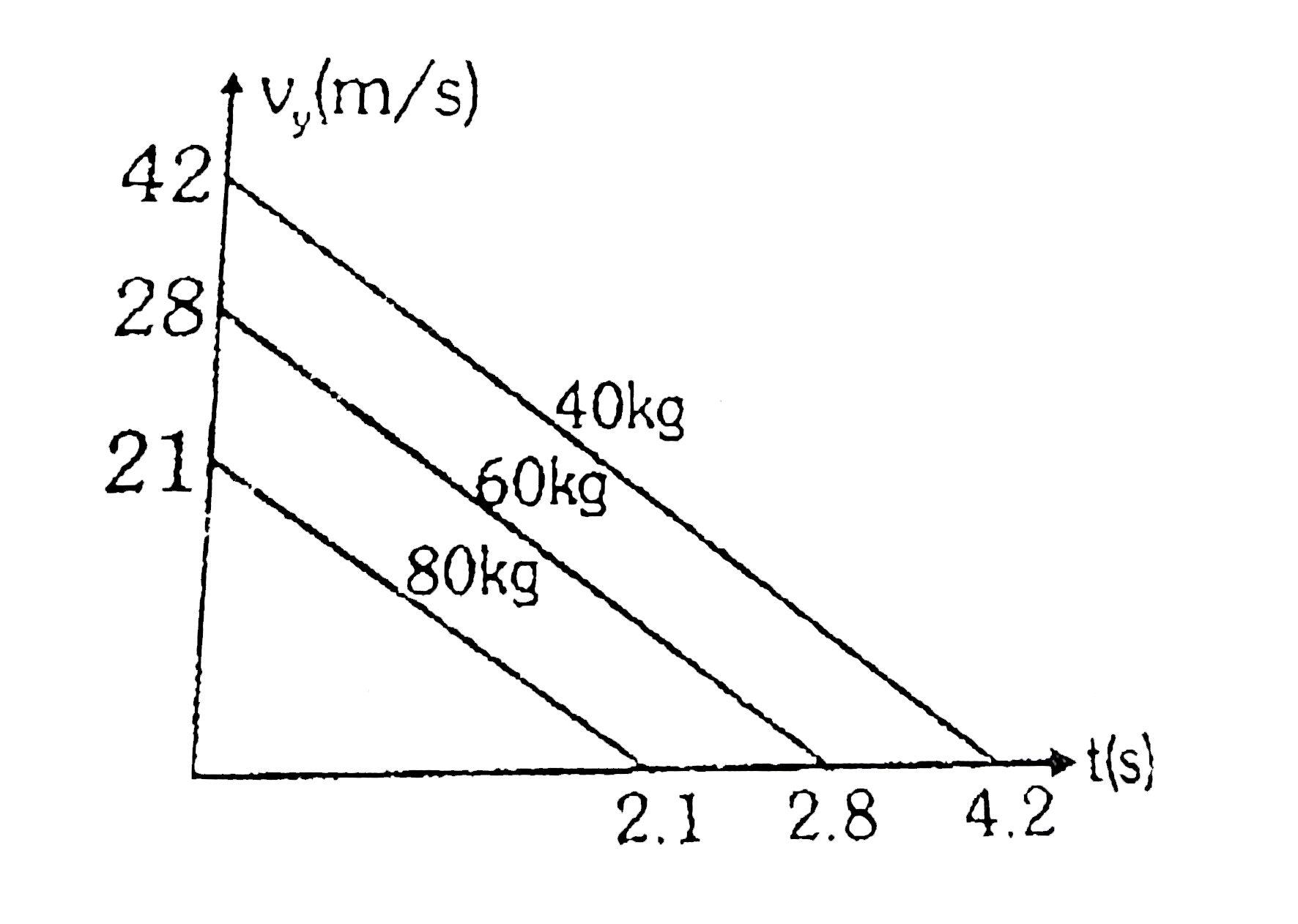
If the clown's mass is 80kg, what initial velocity v0 will have as he leaves the cannot?View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the angle the cannot makes with the horiaontal is increased from 45∘, the hoop will have to beView SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the mass of a clown doubles, his initial kinetic energy, mv20/2, will :-View Solution
