Question

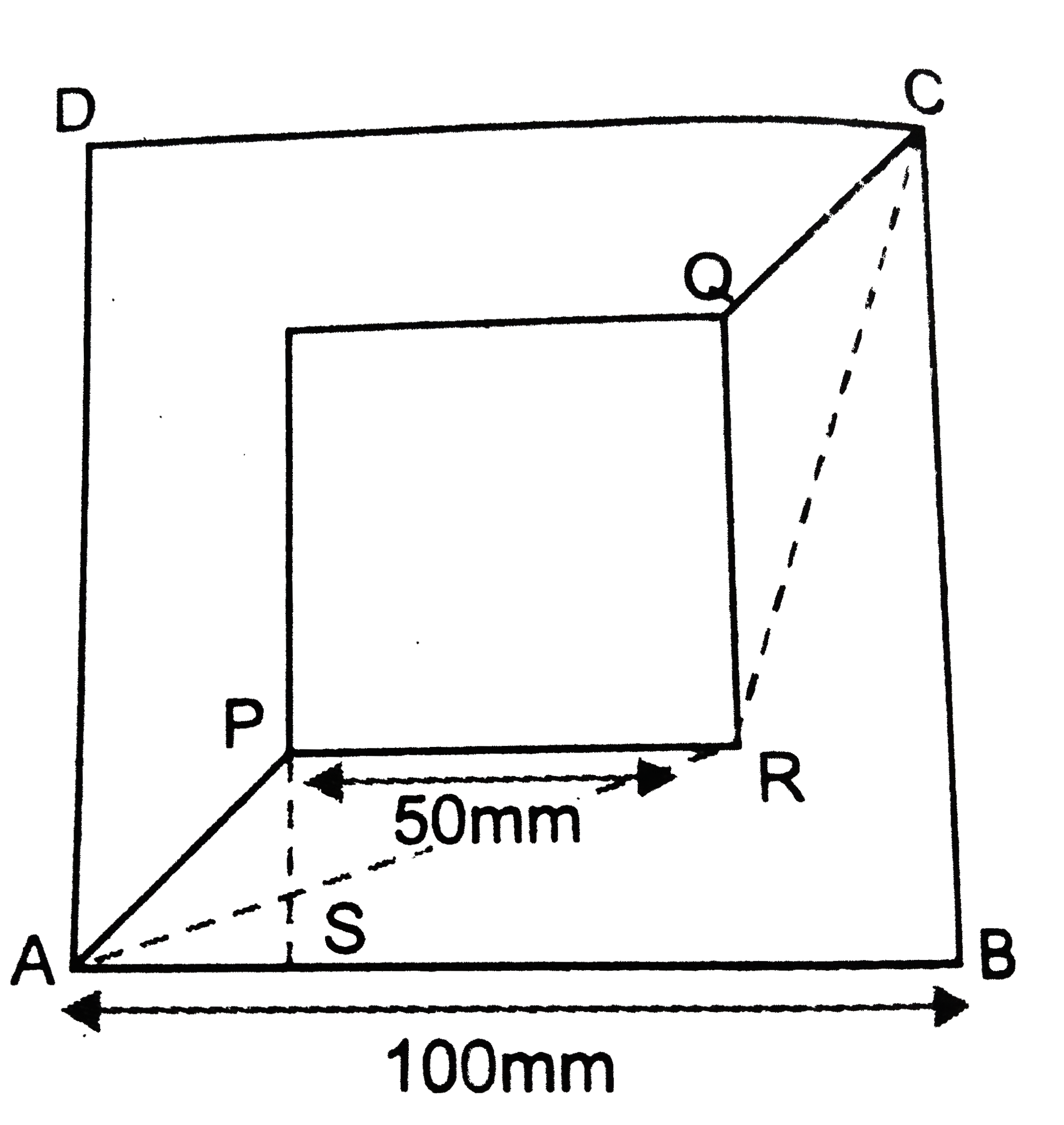
A man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of $50m\times 50m$ is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s $(v<1)$. What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?

Explanation

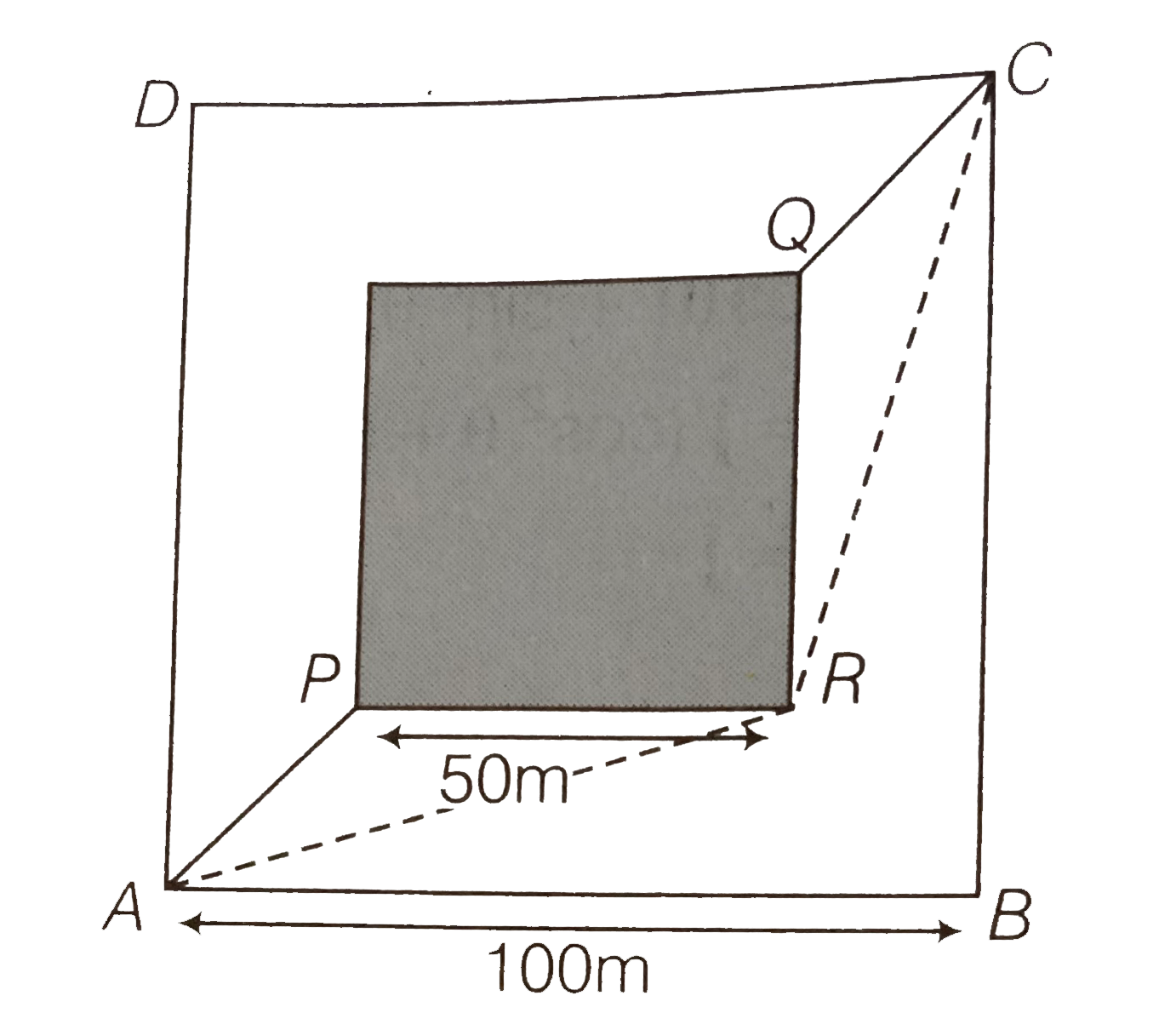
In Fig, 2 (EF) , 35, ` AR= sqrt (AT^2 + TR^2) = sqrt 75^2 + 25 ^2 ) = 25 sqrt 10 = RC`
Total path ` =AR + RC = 2 AR = 50 sqrt 10 m`
Time soutside sand , ` T_0ut) = ( 50 sqrt (10 m)/( 1 m//s) = 50 sqrt (10 s`
` AP= QC = sqrt ( AS^2 + sP^2) = sqrt (25 ^2 + 50 sqrt 2 m`
In sand , ` T_(sand ) = (AP+ QC)/1 + (PQ)/v`
` =(25 sqrt 2 + 25 sqrt 2) /1 + (5) sqrt 2)/v = 50 sqrt 2 [ 1 + 1/v]`
Since ` T_(sand) lt T_(out)`
:. ` 50 sqrt 2 (1 = 1/v) lt 50 sqrt 10`
or ` sqrt 2 ( 1 + 1/v ) lt sqrt 10 ` or ` (1 + 1/v ) lt (sqrt 10 )/(sqrt 2) = sqrt 5 ` or ` 1/v lt sqrt 5 - 1 or ` vlt 1/(sqrt 5-1) ~~ 0.81 m//s`.