A mass 1 kg is attaced to the hook of a spring and the spring is suspended vertically from a ceiling (see Fig. 5.12a). The spring is displaced from its equilibrium position by a distance x. The spring constant of the spring is 2.0×102 N/m. Calculate the displacement x.
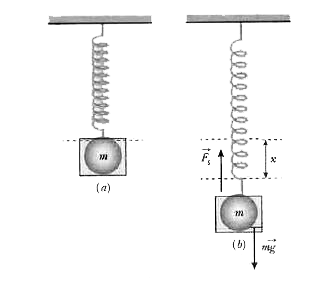
Figure 5-12 (a) Mass of 1 kg attached to a spring is suspended vertically. (b) Spring displace from equilibrium position by a distance x.
(1) In Fig. 5-12, mass attached to the spring is shown. Figure 5-12a shows the relaxed position of spring. Figure 5-12b shows the distance x by which the spring is stretched due to displacement from equilibrium position. (2) The force on the mass is balanced by its weight acting downwards and spring force acting upwards.
Calculation: At equilibrium, spring force = weight, that is,
→Fs=mg
That is, ∣∣→Fs∣∣=kx=mg
Substituting m = 1 kg, k=2.0×102 N/m and g=10 m/s2, we obtain the displacement x as
x=mgx=(1 kg)(10 m/s2)(2.0×102 N/m)
=5×10−2m=5 cm
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PROBLEMS52videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
 View Solution
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass 5 kg is attached to the hook of a spring balance and the balance is suspended vertically from the roof of a lift. The reading on the spring balance when the lift is going up with an acceleration of 0.25 ms−2 is take, (take, g=10ms−2)
A51.25 NB48.75 NC52.75 ND47.25 N - Question 2 - Select One
A block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
AMg/kB2Mg/kC4Mg/kDMg/2k - Question 3 - Select One
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
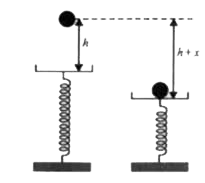 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.
 View Solution
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
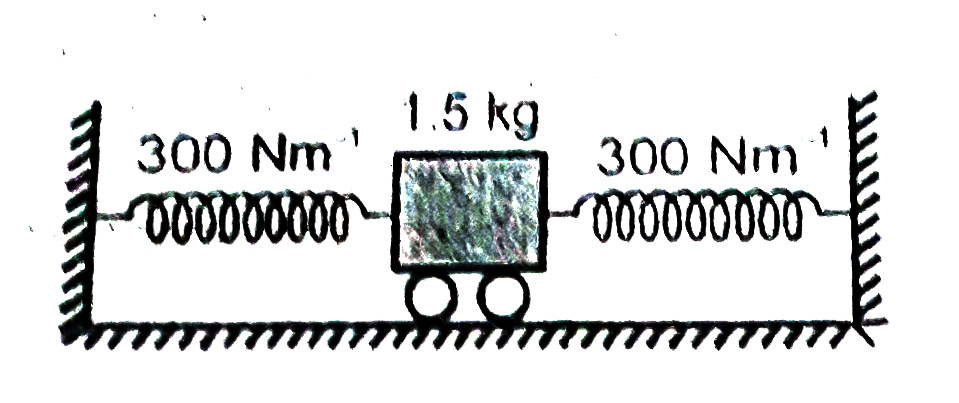 View Solution
View SolutionFigure-1 to Figure -4 shows four different spring arrangements . Mass m in each arrangement is displacement from its equilibrium position and released Neglec mass of the springs. Choose the correct statement (s)
 View Solution
View Solution1 kg weight is suspended to a weightless spring and it has time period T. If now 4 kg weight is suspended from the same spring the time period will be
View Solution

