A mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r Fig.
If the mass is removed futher away such that OP becomes 2h, by what factor the force of gravitational will decrease, if h=r ?
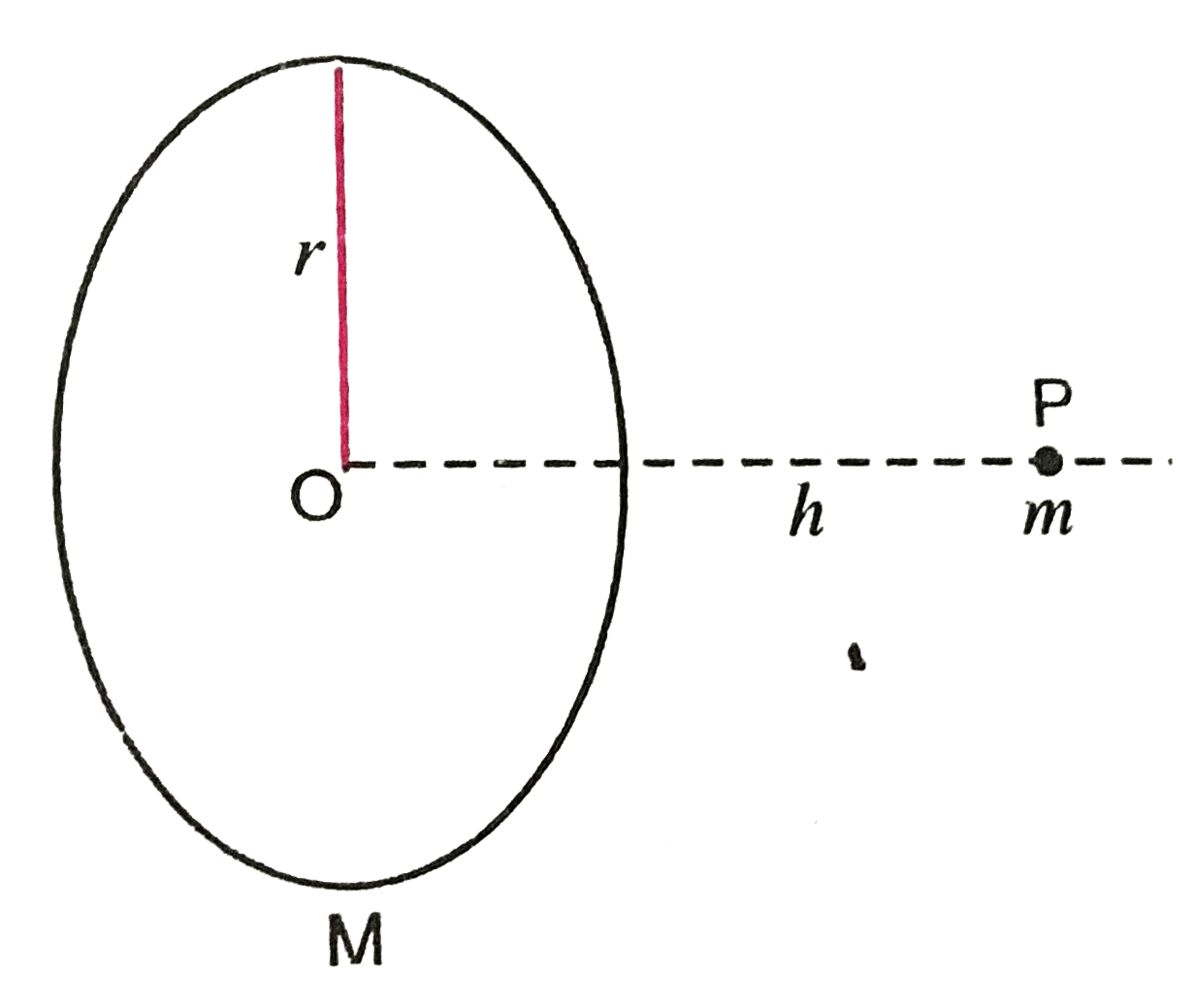
Gravitational force on an object of mass m at point P distance h from centre O lying on the axis of the circular ring of radius r and mass M is given by
F=GMmh(r2+h2)3/2 [See Sol. Q. 15 (HOTS)]
When h=2h, then F'=GMm×2h(r2+4h2)3/2
If h=r, then F=GMmr(r2+r2)3/2=GMm2√2r3 and F'=GMm×2r(r2+4r2)3/2=2GMm5√5r3
∴F'F=4√25√5 or F'=4√25√5
Topper's Solved these Questions
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:SHORT ANSWER QUESTIONS II.
Explore 1 Video
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:SHORT ANSWER QUESTIONS III.
Explore 1 Video
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:SHORT ANSWER QUESTIONS I.
Explore 1 Video
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBook:PRADEEPChapter:BEHAVIOUR OF PERFECT GAS & KINETIC THEORYExercise:Assertion - Reason Type questions
Explore 14 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
Similar Questions
Knowledge Check
The escape velocity form the centre of a unifrom ring of mass M and radius R is :
A√2GMRB√GMRC√GM2RD√GMRFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
A4Gmm0R2BzeroC9Gmm0R2DNone of these
Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View SolutionA particle of mass m is ocated at a distance r from the centre of shell of mass M and radius R. The force between the shell and mass F(r). The plot of F(r) ve r is :
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
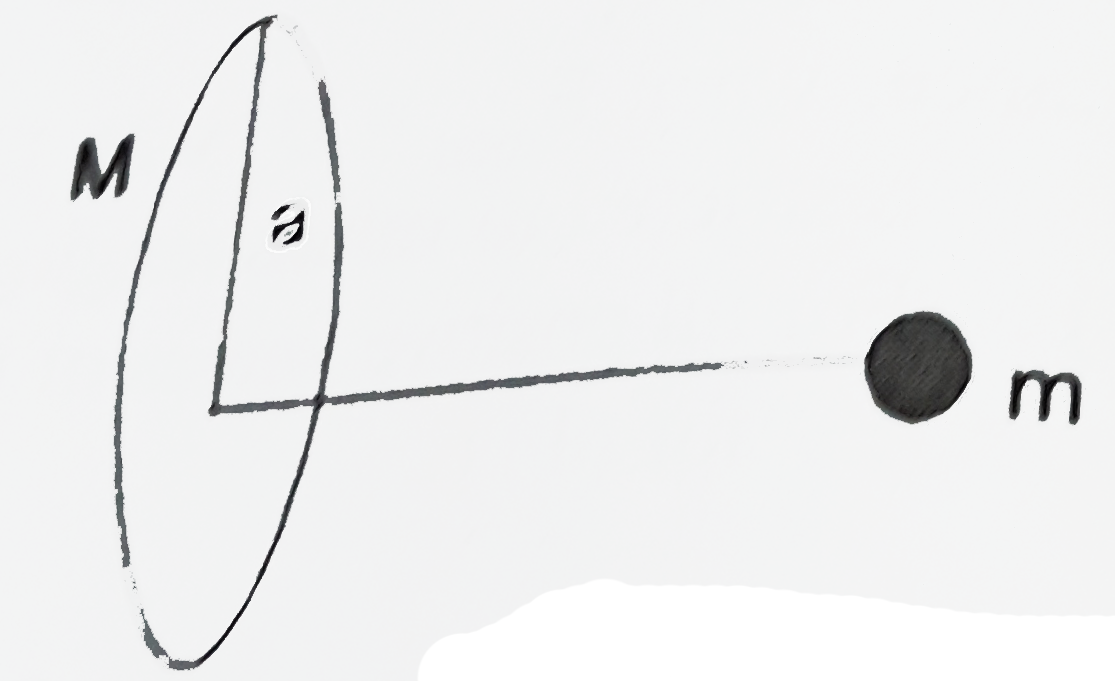
if x<<a, the particle of mass m will:
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
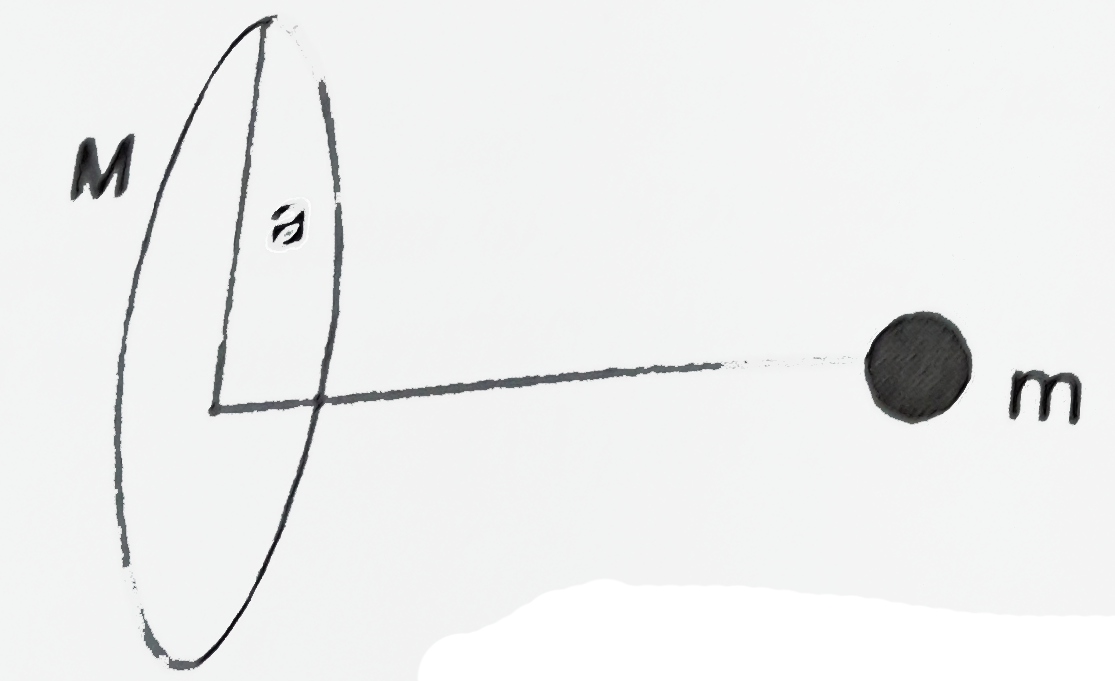
Gravitational potential energy of this system.
View Solution