A mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
0.15m
0.12m
0.5m
0.25m
The correct Answer is:A
To find the maximum compression of the spring when a mass collides with it, we can use the principle of conservation of energy. The kinetic energy of the mass will be converted into the potential energy stored in the spring at maximum compression.
1. Identify the Given Values:
- Mass (m) = 0.5 kg
- Initial speed (v) = 1.5 m/s
- Spring constant (k) = 50 N/m
2. Calculate the Initial Kinetic Energy (KE):
The kinetic energy of the mass can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×0.5kg×(1.5m/s)2
KE=12×0.5×2.25=0.5625J
3. Set Up the Equation for Potential Energy (PE) of the Spring:
The potential energy stored in the spring at maximum compression (x) is given by:
PE=12kx2
4. Apply Conservation of Energy:
At maximum compression, all the kinetic energy will be converted into potential energy:
KE=PE
Therefore:
0.5625=12×50×x2
5. Solve for x:
Rearranging the equation gives:
0.5625=25x2
x2=0.562525
x2=0.0225
Taking the square root of both sides:
x=√0.0225=0.15m
6. Conclusion:
The maximum compression of the spring is:
x=0.15m
- Mass (m) = 0.5 kg
- Initial speed (v) = 1.5 m/s
- Spring constant (k) = 50 N/m
The kinetic energy of the mass can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×0.5kg×(1.5m/s)2
KE=12×0.5×2.25=0.5625J
The potential energy stored in the spring at maximum compression (x) is given by:
PE=12kx2
At maximum compression, all the kinetic energy will be converted into potential energy:
KE=PE
Therefore:
0.5625=12×50×x2
Rearranging the equation gives:
0.5625=25x2
x2=0.562525
x2=0.0225
Taking the square root of both sides:
x=√0.0225=0.15m
The maximum compression of the spring is:
x=0.15m
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion and Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Auto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
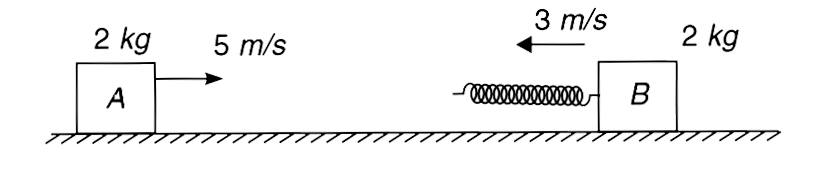
View SolutionA block A of mass 2kg is moving to right with a speed of 5 m/s on a horizontal smooth surface. Another block B of mass 2 kg, with a mass less spring of force constant K=200 N/m attached to it, is moving to left on the same surface with a speed of 3 m/s. Block A collides with the spring attached to B. Calculate
(a) the final velocity of the block A.
(b) the minimum kinetic energy of the system of two blocks during subsequent motion.
(c) Repeat part (b) if there is no spring and the two blocks collide head on. Assume that the blocks are made of perfectly elastic material
View Solution
Knowledge Check
A mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
A0.15 mB0.12 mC1.5 mD0.5 mA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be
 A0.5 mB0.15 mC1.5 mD0.12 m
A0.5 mB0.15 mC1.5 mD0.12 mA car of mass 1000 kg moving with a speed 18kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. The maximum compression of the spring is
A1 mB2 mC3 mD4 m
A 4.0 kg body, moving with a speed of 2.0m/s ,collides with a spring bumper of negligible mass and force constant 100Nm−1 .The maximum compression of the spring is ?
View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

View SolutionA solid cylinder of mass 3 kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be
View SolutionA solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression producec in the spring will be :
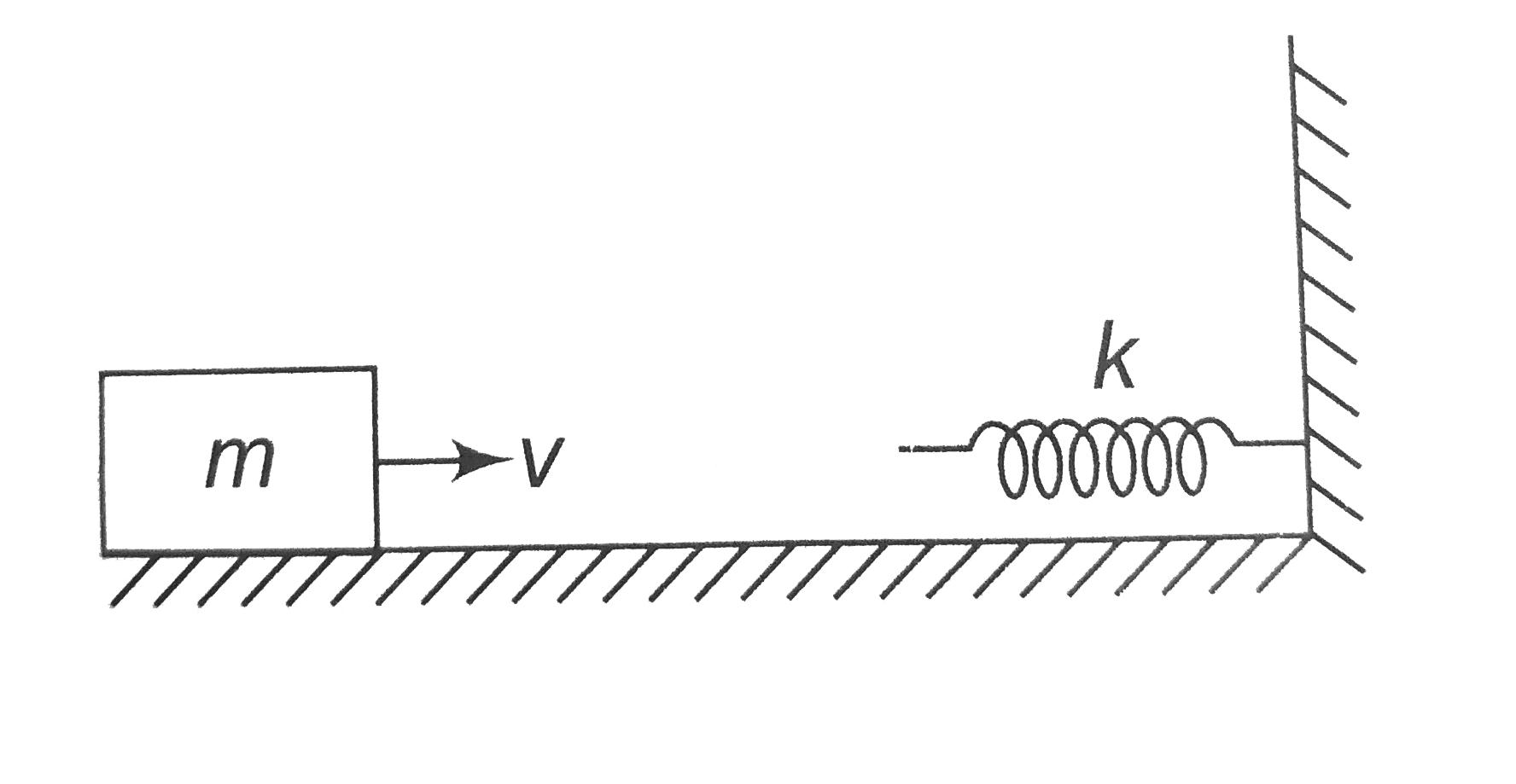
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
View Solution
