A mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
a)0.15m
b)0.12m
c)0.5m
d)0.25m
The correct Answer is:A
To solve the problem of finding the maximum compression of the spring when a mass collides with it, we can follow these steps:
Step 1: Identify the given values
- Mass (m) = 0.5 kg
- Initial speed (v) = 1.5 m/s
- Spring constant (k) = 50 N/m
Step 2: Write the formula for kinetic energy (KE)
The kinetic energy of the mass before it collides with the spring is given by the formula:
KE=12mv2
Step 3: Calculate the initial kinetic energy
Substituting the values into the kinetic energy formula:
KE=12×0.5kg×(1.5m/s)2
KE=12×0.5×2.25=0.5625J
Step 4: Write the formula for potential energy (PE) stored in the spring
The potential energy stored in the spring at maximum compression (x) is given by:
PE=12kx2
Step 5: Set the kinetic energy equal to the potential energy
At maximum compression, all the kinetic energy will be converted into potential energy:
12mv2=12kx2
We can cancel the 12 from both sides:
mv2=kx2
Step 6: Rearrange the equation to solve for x
x2=mv2k
x=√mv2k
Step 7: Substitute the known values into the equation
x=√0.5kg×(1.5m/s)250N/m
x=√0.5×2.2550=√1.12550=√0.0225
Step 8: Calculate the maximum compression
x=0.15m
Conclusion
The maximum compression of the spring is 0.15 m.
- Mass (m) = 0.5 kg
- Initial speed (v) = 1.5 m/s
- Spring constant (k) = 50 N/m
The kinetic energy of the mass before it collides with the spring is given by the formula:
KE=12mv2
Substituting the values into the kinetic energy formula:
KE=12×0.5kg×(1.5m/s)2
KE=12×0.5×2.25=0.5625J
The potential energy stored in the spring at maximum compression (x) is given by:
PE=12kx2
At maximum compression, all the kinetic energy will be converted into potential energy:
12mv2=12kx2
We can cancel the 12 from both sides:
mv2=kx2
x2=mv2k
x=√mv2k
x=√0.5kg×(1.5m/s)250N/m
x=√0.5×2.2550=√1.12550=√0.0225
x=0.15m
The maximum compression of the spring is 0.15 m.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
View Solution
Knowledge Check
A car of mass 1000 kg moving with a speed 18kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. The maximum compression of the spring is
A1 mB2 mC3 mD4 m
Auto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
View SolutionTo stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of 18.0km/h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. What is the maximum compression of the spring?
View SolutionA solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be :
View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
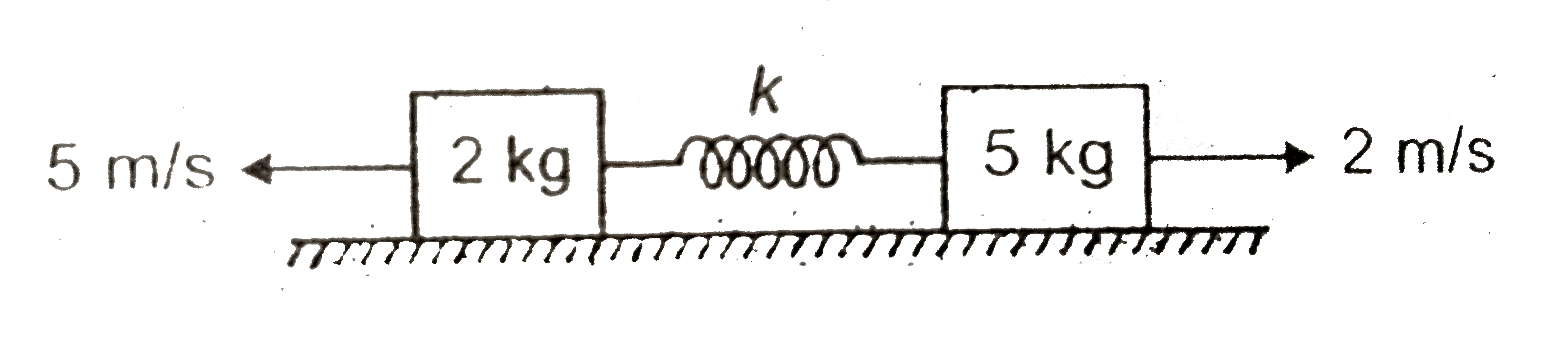
View Solution
