A mass of 1 kg is placed at (1m, 2m, 0). Another mass of 2 kg is placed at (3m, 3m, 0). Find the moment of inertial of both the masses about z-axis
To find the moment of inertia of the two masses about the z-axis, we will follow these steps:
Step 1: Identify the masses and their positions
We have two masses:
- Mass m1=1kg at position (1m,2m,0)
- Mass m2=2kg at position (3m,3m,0)
Step 2: Calculate the perpendicular distances from the z-axis
The moment of inertia I about the z-axis for a point mass is given by the formula:
I=m⋅r2
where r is the perpendicular distance from the z-axis, which can be calculated using:
r=√x2+y2
For mass m1:
- Position: (1,2)
- Calculate r1:
r1=√12+22=√1+4=√5
For mass m2:
- Position: (3,3)
- Calculate r2:
r2=√32+32=√9+9=√18
Step 3: Calculate the moment of inertia for each mass
Now, we can calculate the moment of inertia for each mass about the z-axis.
For mass m1:
I1=m1⋅r21=1⋅(√5)2=1⋅5=5kg m2
For mass m2:
I2=m2⋅r22=2⋅(√18)2=2⋅18=36kg m2
Step 4: Calculate the total moment of inertia
The total moment of inertia I about the z-axis is the sum of the individual moments of inertia:
I=I1+I2=5+36=41kg m2
Final Answer
The moment of inertia of both masses about the z-axis is 41kg m2.
---
We have two masses:
- Mass m1=1kg at position (1m,2m,0)
- Mass m2=2kg at position (3m,3m,0)
The moment of inertia I about the z-axis for a point mass is given by the formula:
I=m⋅r2
where r is the perpendicular distance from the z-axis, which can be calculated using:
r=√x2+y2
- Position: (1,2)
- Calculate r1:
r1=√12+22=√1+4=√5
- Position: (3,3)
- Calculate r2:
r2=√32+32=√9+9=√18
Now, we can calculate the moment of inertia for each mass about the z-axis.
I1=m1⋅r21=1⋅(√5)2=1⋅5=5kg m2
I2=m2⋅r22=2⋅(√18)2=2⋅18=36kg m2
The total moment of inertia I about the z-axis is the sum of the individual moments of inertia:
I=I1+I2=5+36=41kg m2
The moment of inertia of both masses about the z-axis is 41kg m2.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.2
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.3
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The point masses of 0.3 kg, 0.2 kg and 0.1 kg are placed at the corner of a right angles ΔABC, as shown in Fig. 8.49. find the moment of inertia of the system (i) about an axis through A and perpendicular to the plane of the diagram and (ii) about an axis along BC.
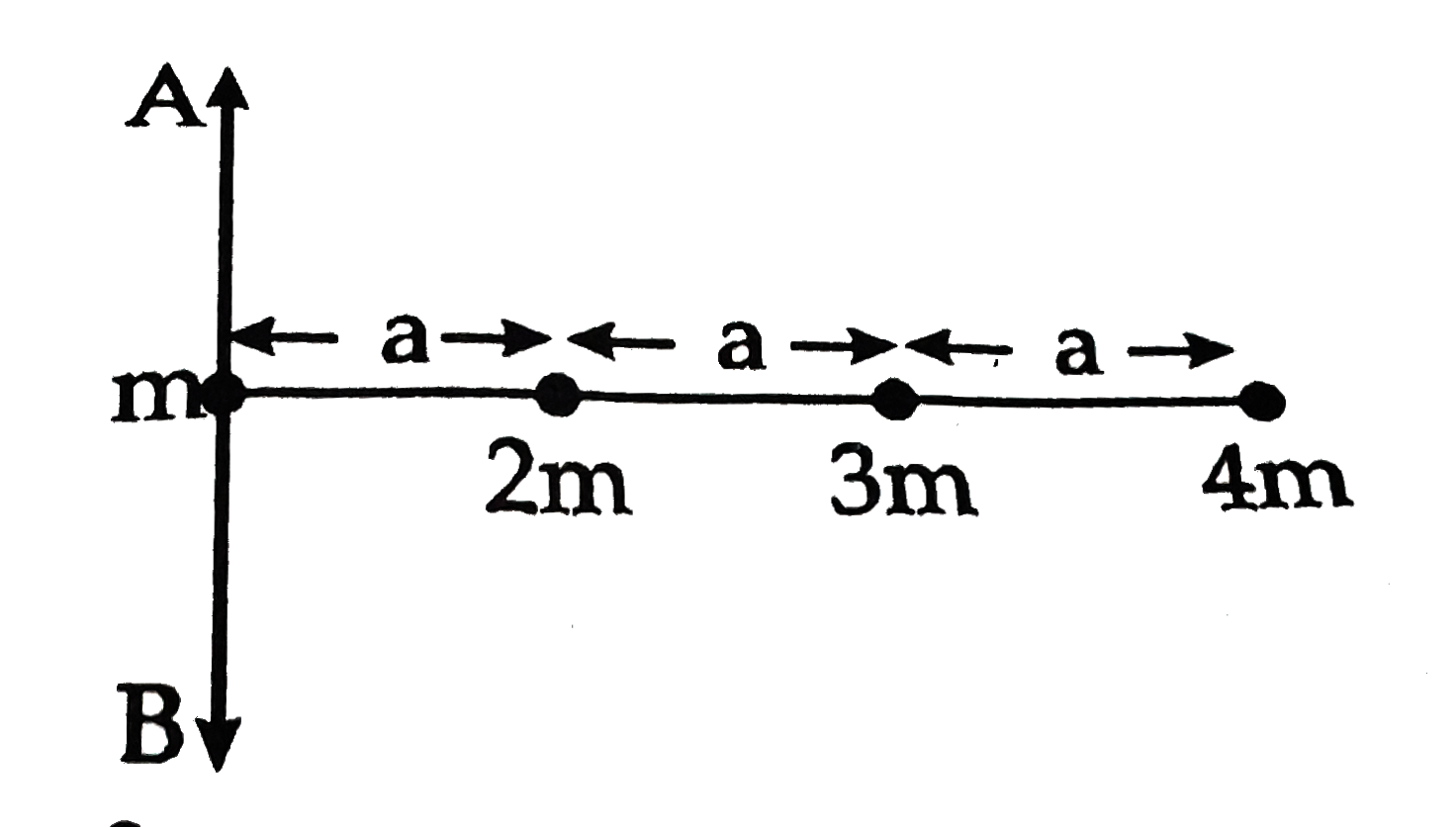
View SolutionFour masses m, 2 m, 3 m and 4 m are connected by a rod of negligible mass. The moment of inertia of the system about the axis AB is
View Solution
Knowledge Check
A particle of mass 1 kg is kept at (1m,1m,1m). The moment of inertia of this particle about Z-axis would be
A1kg-m2B2kg-m2C3kg-m2DNone of theseParticles each of mass 1kg are placed at 1m, 2m and 4m on X-axis with respect to origin. Then moment of inertia of the system about Y-axis is
A7kgm2B14kgm2C21kgm2D28kgm2Three thin rods, each of length 2 m and mass 3 kg are placed along x, y and z axes, such that one end of each rod is at the origin. The moment of inertia of this system about the x axis is
A2kgm2B4kgm2C6kgm2D8kgm2
Three point masses, each of mass 2kg are placed at the corners of an equilateral triangle of side 2m. What is moment of inertia of this system about an axis along one side of a triangle?
View SolutionEach point mass 2 kg is connected at the end of each uniform rod of length 1m and mass 1kg. All the masses are in XY plane. Find the moment of inertia of system about Z-axis (in kg-m2).
View SolutionTwo objects of masses 1kg and 2kg separated by a distance of 1.2m are rotating about their centre of mass. Find the moment of inertia of the system
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionThe centre of mass of three particle of masses 1 kg , 2 kg and 3 kg is at (2,2,2). The position of the fourth mass of 4 kg to be placed in the system such that the new centre of mass is at (0,0,0) is
View Solution
