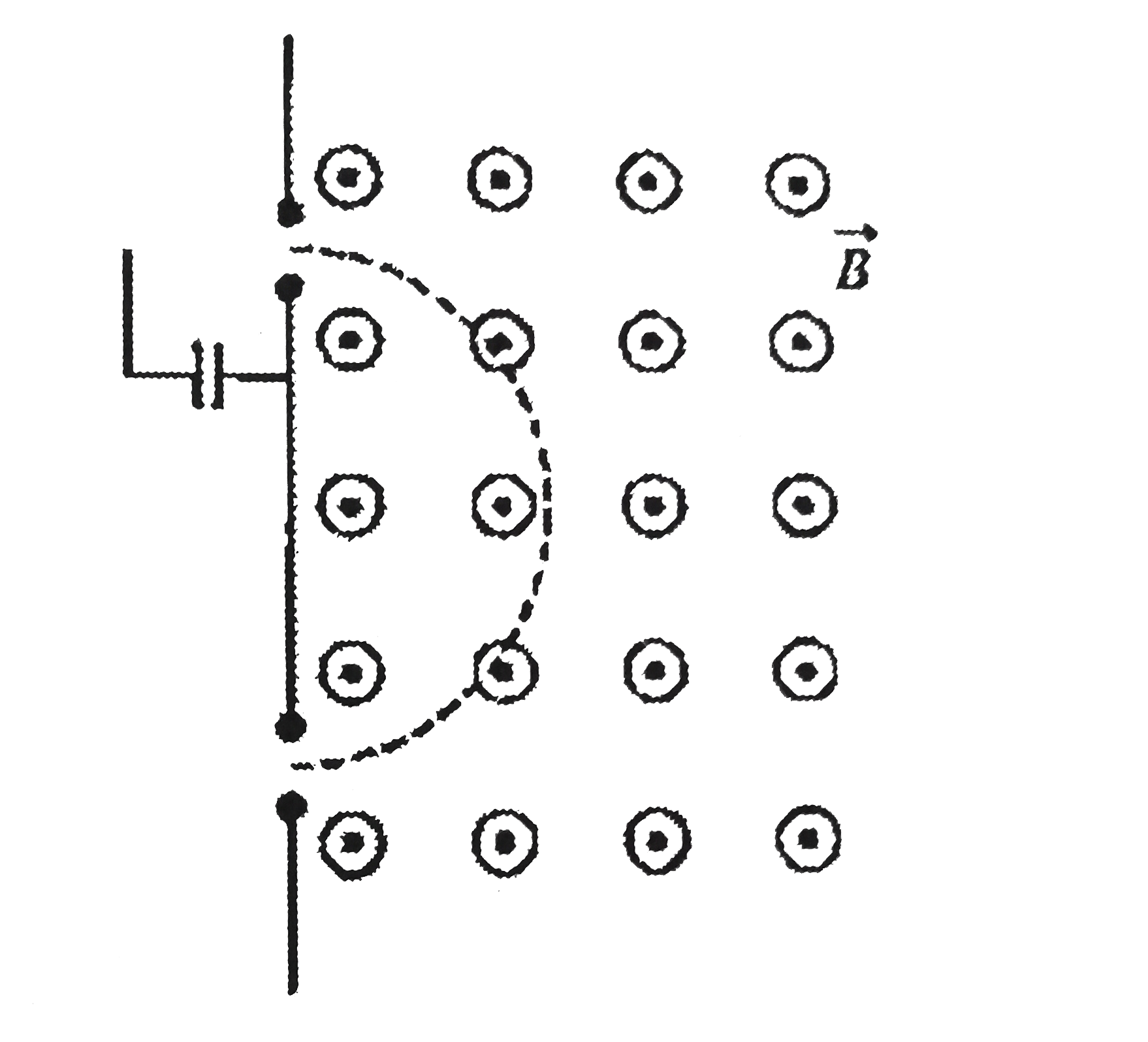
A mass spectrometer is a device which selelct particle of equal mass. An ion with an electric charge q>0. Starts at rest from s ource S and is accelerated through a potential difference V. it passes thorugh a hole into a region of constant magnetic field →B perpendicular to the plane of the paper as shown in the figure. The particle is deflected by the magnetic field and emerges thorugh the bottom hole at a distance d from the top hole. The mass of the particle is:
(1) Because the (uniform magnetic field causes the (charged) ion to follow a circular path, we can relate the ion.s mass m to the path.s radius r with (r=mv|q|B). From Fig. we see that r = x/w (the radius is half the diameter). From the problem statement,
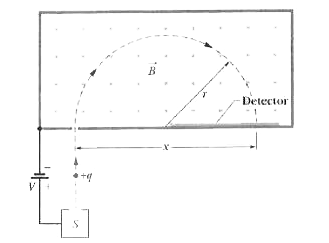
A positive ion is accelerated from its sources S by a potential difference V, enters a chamber of uniform magnetic field →B, travels through a semicircle of radius r, and strikes a detector at a distance x.
We know the magnitude B of the magnetic field. However, we lack the ion.s speed v in the magnetic field after the ion has been accelerated due to the potential difference V. (2) To relate v and V, we use the fact that mechanical energy (Emec=K+U) is conserved during the acceleration.
Finding speed. : When the ion emerges from the source, its kinetic energy is approximately zero. At the end of the acceleration, its kinetic energy is 1/2mv2. Also, during the acceleration, the positive ion moves through a change in potential of -V. Thus, because the ion has positive charge q, its potential energy changes by -qV. If we now write the conservation of mechanical energy as
ΔK+ΔU=0,
we get
12mv2−qV=0
or v=√2qVm
Finding mass : Substituting this value for v into Eq. 28-8 given us
r=mvqB=mqB√2qVm=1B√2mVq.
Thus, x=2r=2B√2mVq.
Solving this for m and substituting the given data yield
m=B2qx28V
=(0.080000T)2(1.6022×10−19C)(1.6254m)28(1000.0V)
=3.3863×10−25kg=203.93u.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Check point6videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Problems49videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
Similar Questions
A mass spectrometer is a device which selelct particle of equal mass. An ion with an electric charge q>0. Starts at rest from s ource S and is accelerated through a potential difference V. it passes thorugh a hole into a region of constant magnetic field →B perpendicular to the plane of the paper as shown in the figure-4.233. The particle is deflected by the magnetic field and emerges thorugh the bottom hole at a distance d from the top hole. The mass of the particle is:
 View Solution
View SolutionA proton and α−partic≤ are accelerated with same potential difference and they enter in the region of constant magnetic field B perpendicular to the velocity of particles. Find the ratio of radius of curvature of alpa−partic≤.
View Solution
Knowledge Check
- Question 1 - Select One
An α− particle moves from E to W in a magnetic field perpendicular to the plane of the paper and into the paper. The particle is defelcted towards
AEastBWestCSouthDNorth - Question 2 - Select One
A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
Aincreases the K.E. of the particleBdecreases the K.E. of the particleCchanges the direction of motion of the particleDdoes both (a) and ( c) - Question 3 - Select One
A charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
A(√Vm2qB2)B2VmqB2C√2Vmq(1B)D√Vmq(qB)
A charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA charged particle having mass m and charge q is accelerated by a potential difference V, it flies through a uniform transverse magnetic field B. The field occupies a region of space d. Fnd the time interval for which it remains inside the magnetic field.
View SolutionAn ion of charge + g and mass m is accelerated in a region of potential difference V volts and then it enters a region of uniform magnetic field B perpendicular to its velocity. If the ion describes a semicircle of diameter x, then its mass m is
View SolutionA particle of mass m carrying charge q is accelerated by a potential difference V. It enters perpendicularly in a region of uniform magnetic field B and executes circular arc of radius R, then qm equals
View SolutionA particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View Solution

