A massles spool of inner radius r and other radius R is placed against vertical wall and tilted split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hanging. There exists no friction at point A, while the coefficient of friction between spool and point B is μ. The angle between two surface is θ

The magnitude of the force on the spool at B in order to maintain equilibrium is mg√(rR)2+(1−rR)21tan2θ
The magnitude of the force on the spool at B in order to maintain equilibrum is mg(1−rR)1tanθ
The minimum value of μ for the system to remain in equilibrium is cotθ(R/r)−1
The minimum values of μ for the system to remain in equilibrium is tanθ(R/r)−1
The correct Answer is:A, D
mgr=fR………..i
N1sinθ+f=mg ………………ii
N1cosθ=N2……………..iii

From eqn i. f=mgrR
From eqn ii and iii N2=mg−ftanθ=mgtanθ[1−rR]
Net force at B:fB=√f2+N22
For the minimum value of μ:f≤μN2
⇒mgrr≤μmgtanθ[1r/R]
⇒μ≥tanθR/r−1)
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
A massless spool of inner radius r outer radius R is placed against a vertical wall and a titled split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hainging. There exists no friction at point A, while the coefficient of friction between the spool and point B is μ. The angle between the two surface is θ

View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
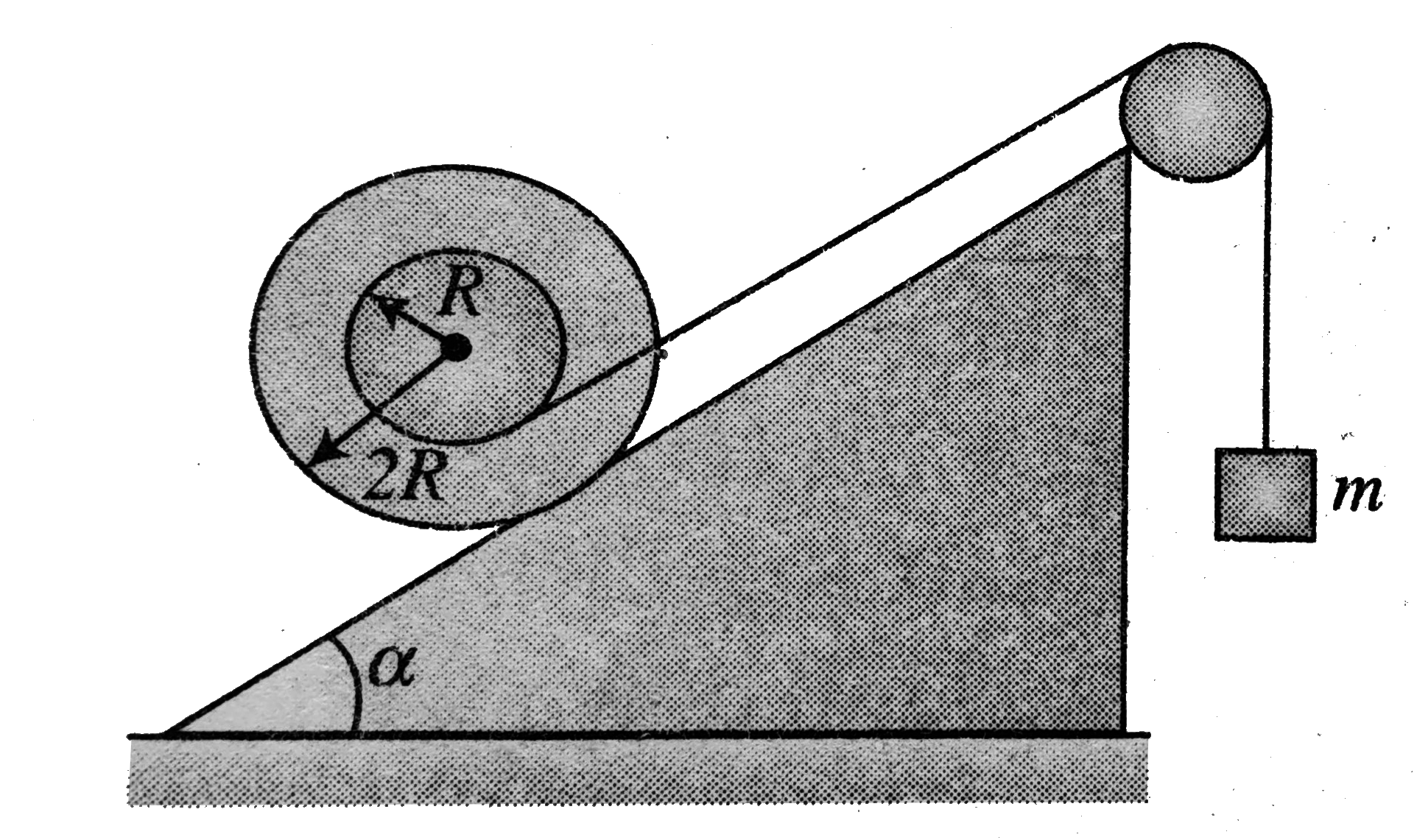
View SolutionA spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is
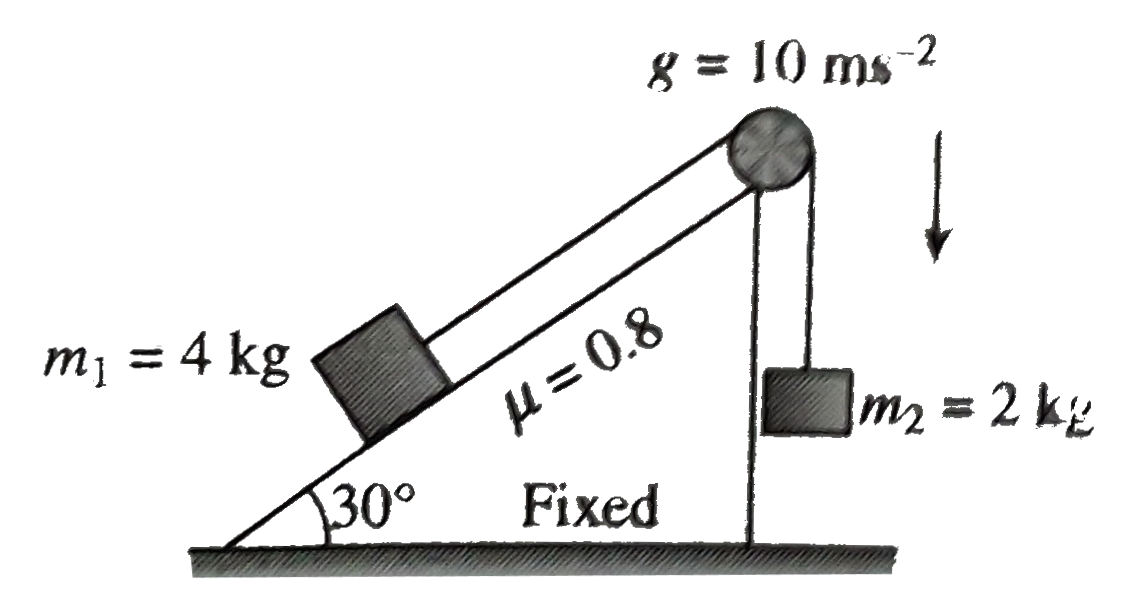
View SolutionTwo blocks of masses m1 and m2 are connected through a massless inextensible string .A block of mass m1 is placed at the fixed rigid inclined surface while the block of mass m2 hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m1 and m2 released from rest
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
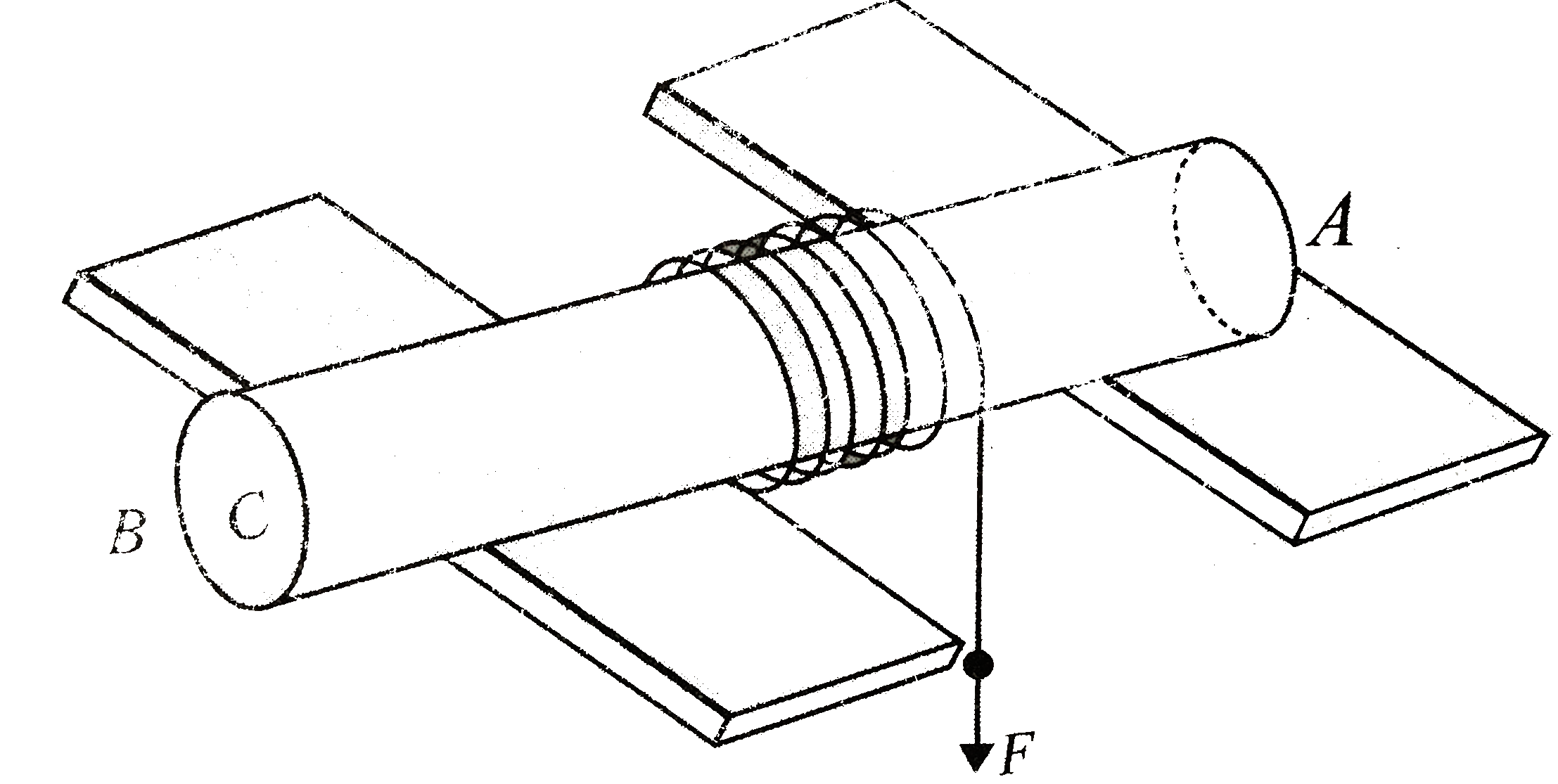
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA block of mass m=1kg has a speed v=4m/s at θ=60∘ on a circular track of radius R = 2 m as shown in figure. Size of the block is negligible. Coefficient of friction between block and the track is μ=0.5. The force of friction between the two is

View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View Solution
