A massless rod S having length 2l has equal point masses attached to its two ends as shown in figure. The rod is rotating about an axis passing through its centre and making angle α with the axis. The magnitude of change of momentum of rod i.e., ∣∣∣dLdt∣∣∣ equals
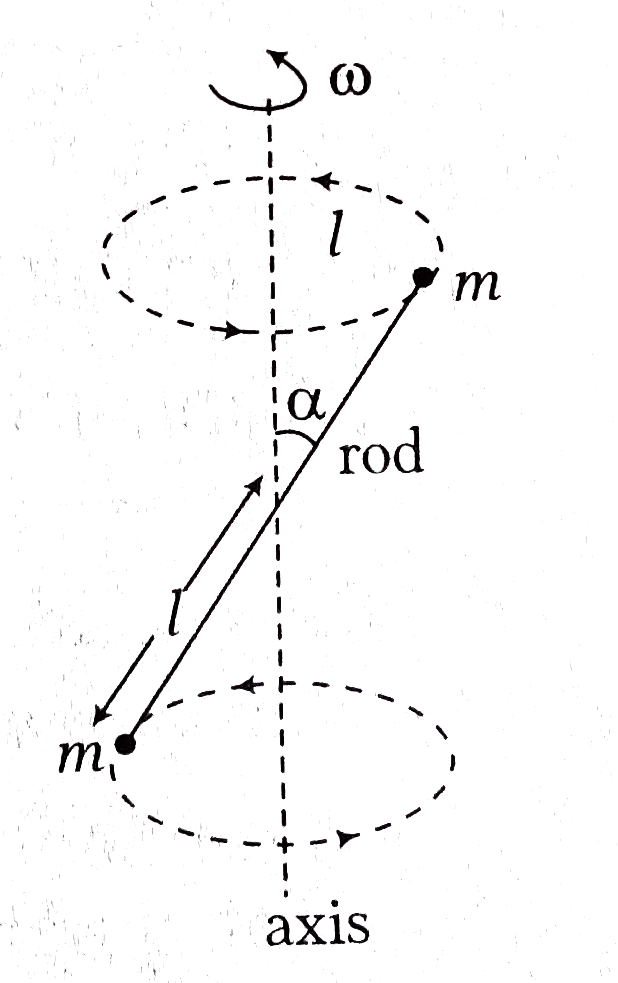
2ml3ω2sinθ.cosθ
ml2ω2sin2θ
ml2sin2θ
m1/2l1/2ωsinθ.Cosθ
The correct Answer is:B
The radius of the circular followed by the masses is r=lsinα
As, angular momentum, L=r×p=r×mv
⇒|L|=lsinθ(mωlsinθ)
On differentiating, we get
d|L|dt=mωl22sinθ.cosθdθdt
⇒∣∣∣dLdt∣∣∣=2ml2ω2sinθ.cosθ=ml2ω2sin2θ.
Topper's Solved these Questions
Similar Questions
The moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is

View Solution
Knowledge Check
A massless rod S having length 2l has equal point masses attached to its two ends as shown in figure. The rod is rotating about an axis passing through its centre and making angle α with the axis. The magnitude of change of momentum of rod i.e., ∣∣∣dLdt∣∣∣ equals
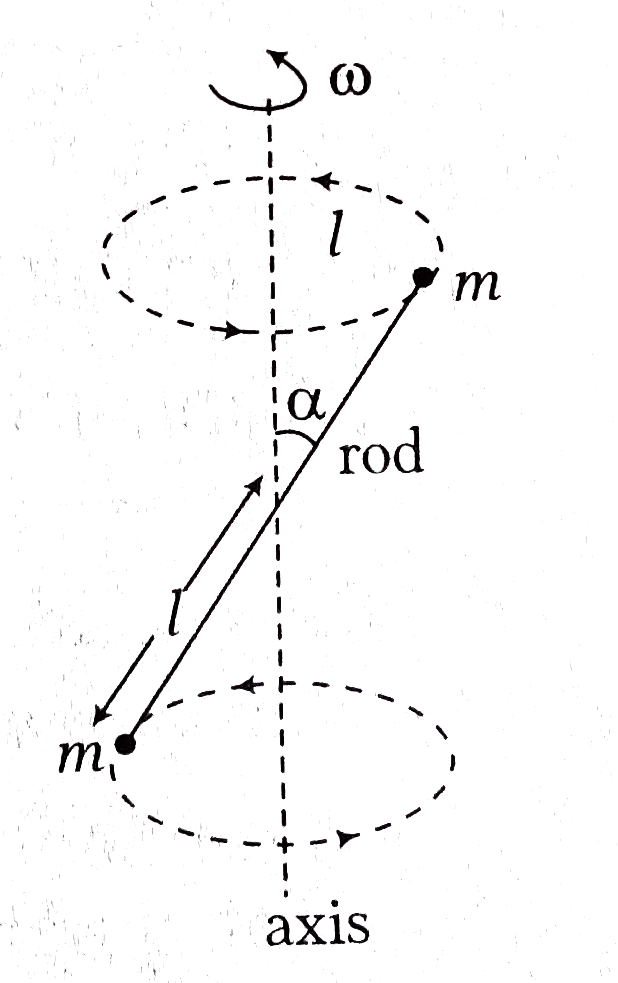 A2ml3ω2sinα.CosαBml2ω2sin2αCml2sin2αDm1/2l1/2ωsinα.cosα
A2ml3ω2sinα.CosαBml2ω2sin2αCml2sin2αDm1/2l1/2ωsinα.cosαThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL√12BL2√12CL√3DL√2The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL2√3BL212CL√3DL√2
if rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
View SolutionThe radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
View SolutionThe M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution