A massless spring of force constant 1000Nm−1 is compressed a distance of 20cm between discs of 8kg and 2kg, spring is not attached to discs. The system is given an initial velocity 3ms−1 perpendicular to length of spring as shown in the figure. What is ground frame velocity of 2kg block (in ms−1) when spring regains its natural length.

The correct Answer is:5
Let v1 and v2 are the velocities along the spring of A and B when spring regains it natural length then
2v1=8v2…….i
122v21+128v22=121000(20100)2…………ii
Form i and ii v1=4ms−1,v2=1ms−1
Ground frame velocity of A
√v2+v21=√32+42=5ms−1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE
12 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension
105 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two blocks of masses m=2kgandm=8kg are connected to a spring of force constant K=1kN/m. The spring is compressed by 20cm and the two blocks are held in this position by a string. The system is placed on a horizontal smooth surface and given a velocity u=3m/s perpendicular to the spring. The string snaps while moving. Find the speed of the block of mass m when the spring regains its natural length.
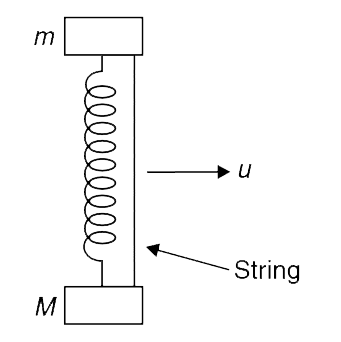
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is of the order of :

View Solution
Knowledge Check
A block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
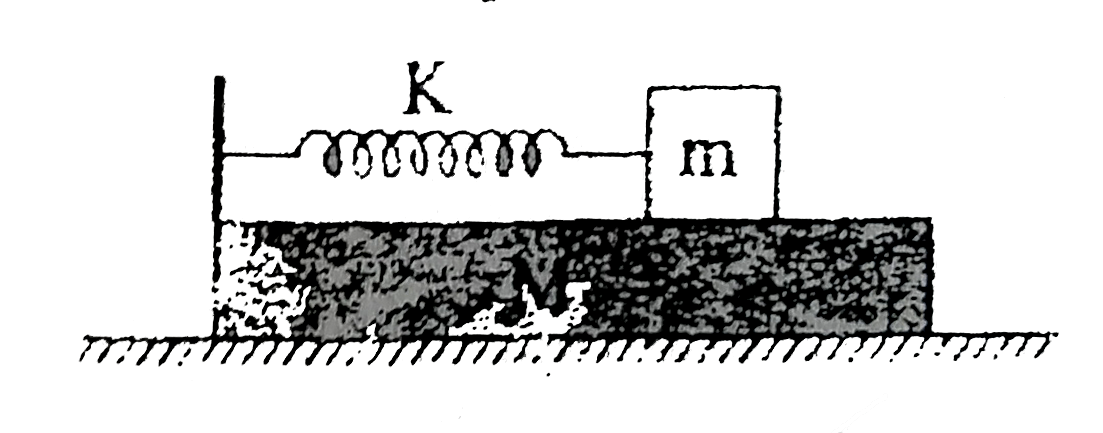 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthA(a) 5ms−1B(b) 3ms−1C(c) 6ms−1D(d) None of theseOne end of an ideal spring of unstreched length lO=1m, is fixed on a frictionless horizontal table. The other end has a small disc of mass 0.1kg attached to it. The disc is projected with a velocity υ0=11m/s perpendicular to the spring.

What is the force constant of spring?A210N/mB100N/mC110N/mD200N/m
Two point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is of the order of :

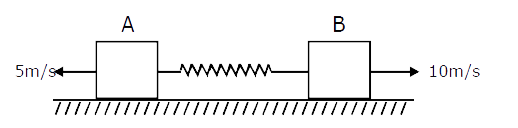
View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionTwo point masses of 3 kg and 6 kg are attached to opposite ends of horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is approximately
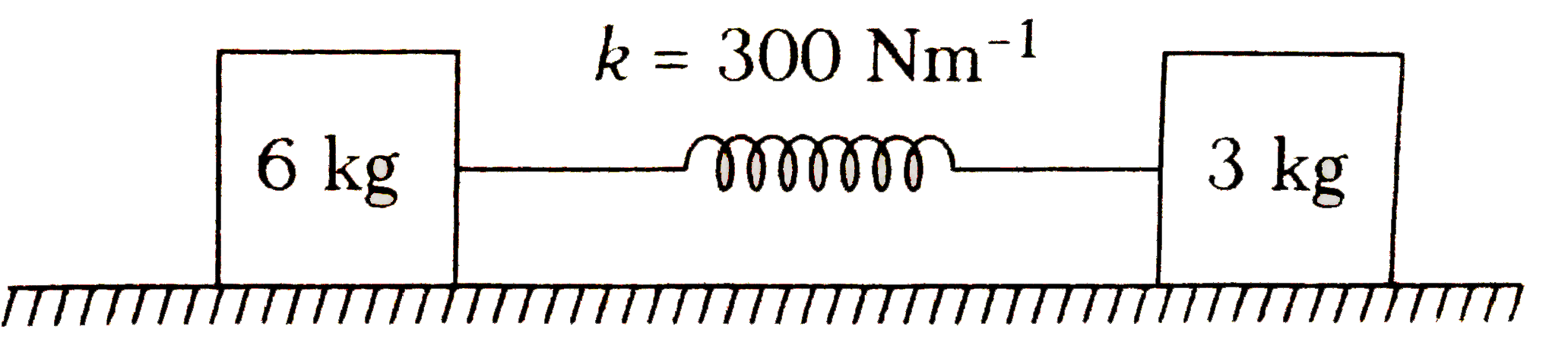
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View Solution
