A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
$λ_{1} = 3650 Å, λ_{2} = 4047 Å, λ_{3} = 4358 Å, λ_{4} = 5461 Å, λ_{5} = 6907 Å$ ,
The stopping voltages, respectively, were measured to be:
$V_{01} = 1.28 V, V_{02} = 0.95 V, V_{03} = 0.74 V, V_{04} = 0.16 V, V_{05} = 0 V$
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be $1.6 \times 10^{- 19} C$ ). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

(a)From frequency $v = \frac{c}{λ}$ ,
$V_{1} = \frac{c}{λ_{1}} = \frac{3 \times 10^{8}}{3650 \times 10^{- 10}} = 8.219 \times 10^{14} H z$
$V_{2} = \frac{c}{λ_{2}} = \frac{3 \times 10^{8}}{4047 \times 10^{- 10}} = 7.412 \times 10^{14}$ Hz
$V_{3} = \frac{c}{λ_{3}} = \frac{3 \times 10^{8}}{4358 \times 10^{- 10}} = 6.884 \times 10^{14}$ Hz
$V_{4} = \frac{c}{λ_{4}} = \frac{3 \times 10^{8}}{5461 \times 10^{10}} = 5.493 \times 10^{14} H z$
$V_{5} = \frac{c}{λ_{5}} = \frac{3 \times 10^{8}}{6907 \times 10^{- 10}} = 4.343 \times 10^{14}$ Hz
$∴$

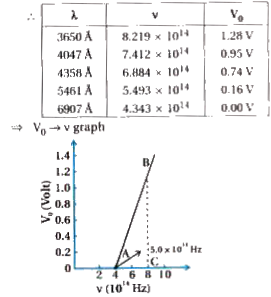
Slope of graph= $\frac{B C}{A C}$
$\frac{Δ V_{0}}{Δ V} = \frac{1.28 - 0}{(8.2 - 5.0) \times 10^{14}}$
$= \frac{1.28}{302 \times 10^{14}} = 0.4 \times 10^{- 14}$
$= 4 \times 10^{- 15}$ Vs
$\Rightarrow$ From Einstein.s photoelectric equation,
$e V_{0} = h V - ϕ_{0}$
$∴ e Δ V_{0} = h Δ V [∵ ϕ_{0} = c o n s \tan t]$
$∴ \frac{Δ V_{0}}{Δ V} = \frac{h}{e}$
$∴ h = e \times \frac{Δ V_{0}}{Δ v}$
$= 1.6 \times 10^{- 19} \times 4.0 \times 10^{- 15}$
$= 6.4 \times 10^{- 34} J s$
(b)Threshold frequency,
$V_{0} = 5.0 \times 10^{14}$ Hz
Which is obtained from $V_{0} \to v$ graph.
Work function.
$ϕ_{0} = h v_{0}$
$= 6.63 \times 10^{- 34} \times 5 \times 10^{14}$
$= 33.15 \times 10^{- 20} J$

|

Updated on:21/07/2023

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-DUAL NATURE OF RADIATION AND MATTER-Section-B Numerical from textual Exercise(Additional Exercise)

Home
Ask Doubt
Profile