A metal ball (density is dropped in water, while another metal ball (density is dropped in a liquid of density . If both the balls have the same diameter and attain the same terminal velocity, the ratio of viscosity of water to that of the liquid is
2
0.5
4
0.25
The correct Answer is:B
To solve the problem, we will use the concept of terminal velocity and the relationship between the densities of the balls and the fluids they are dropped into.
1. Understanding Terminal Velocity:
The terminal velocity Vt of a sphere falling through a fluid is given by the equation:
Vt=29R2(ρb−ρm)gη
where:
- R = radius of the ball
- ρb = density of the ball
- ρm = density of the medium (fluid)
- g = acceleration due to gravity
- η = coefficient of viscosity of the medium
2. Setting Up Equations for Each Ball:
For ball B1 (density ρb1=3.2g/cm3, in water with ρm1=1g/cm3):
Vt1=29R2(3.2−1)gη1
For ball B2 (density ρb2=6.0g/cm3, in liquid with ρm2=1.6g/cm3):
Vt2=29R2(6.0−1.6)gη2
3. Equating Terminal Velocities:
Since both balls attain the same terminal velocity (Vt1=Vt2):
29R2(3.2−1)gη1=29R2(6.0−1.6)gη2
The 29R2g terms cancel out:
(3.2−1)η1=(6.0−1.6)η2
4. Substituting Values:
Calculate the differences in densities:
3.2−1=2.2and6.0−1.6=4.4
Therefore, we have:
2.2η1=4.4η2
5. Finding the Ratio of Viscosities:
Rearranging gives:
η1η2=2.24.4=12
6. Final Result:
Thus, the ratio of the viscosity of water to that of the liquid is:
η1η2=0.5
The terminal velocity Vt of a sphere falling through a fluid is given by the equation:
Vt=29R2(ρb−ρm)gη
where:
- R = radius of the ball
- ρb = density of the ball
- ρm = density of the medium (fluid)
- g = acceleration due to gravity
- η = coefficient of viscosity of the medium
For ball B1 (density ρb1=3.2g/cm3, in water with ρm1=1g/cm3):
Vt1=29R2(3.2−1)gη1
For ball B2 (density ρb2=6.0g/cm3, in liquid with ρm2=1.6g/cm3):
Vt2=29R2(6.0−1.6)gη2
Since both balls attain the same terminal velocity (Vt1=Vt2):
29R2(3.2−1)gη1=29R2(6.0−1.6)gη2
The 29R2g terms cancel out:
(3.2−1)η1=(6.0−1.6)η2
Calculate the differences in densities:
3.2−1=2.2and6.0−1.6=4.4
Therefore, we have:
2.2η1=4.4η2
Rearranging gives:
η1η2=2.24.4=12
Thus, the ratio of the viscosity of water to that of the liquid is:
η1η2=0.5
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A small metal ball of diameter 4mm and density 10.5g/cm3 in dropped in glycerine of density 1.5g/cm3. The ball attains a terminal velocity of 8cms−1. The coefficient of viscosity of glycerine is
View SolutionA small metal ball of diameter 4mm and density 10.5g/cm3 in dropped in glycerine of density 1.5g/cm3. The ball attains a terminal velocity of 8/cms−1. The coefficient of viscosity of glycerine is
View Solution30 mL of methyl alcohol (density = 0.8 g/cc) is mixed with 70 mL of water (density = 1.0 g/cc) at 25∘C to give a solution of density 0.94 g/cc. Find the mole fraction, molarity and molality.
View SolutionA smooth spherical ball of radius 1cm and density 4×103kg/m3 is dropped gently in a large container containing viscous liquid of density 2×103kg/m3, and η=0.1N−s/m2. The distance moved by the ball in t=0.1sec after it attains terminal velocity is

View SolutionA body of density 2.5g/cm3 is let free in a liquid of density 1.25g/cm3 . The downward acceleration of the of the body while sinking in the liquid is . _______
View SolutionA sphere of radius R is gently dropped into liquid of viscosity η in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2R when dropped into the same liquid, will attain its teriminal velocity.
View Solution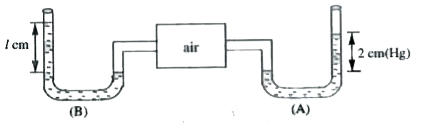
What is l if the liquid in manometre 'B' has a density 1.36 gm/cc.
View SolutionA container filled with a liquid of density 4p as shown in the figure. The velocity efflux through orifice is (ρ is density of water and g = 10 ms−2)
_PHY_E05_013_Q01.png)
View SolutionTwo balls of masses 2 g and 6 g are moving with kinetic energy in the ratio of 3:1. What is the ratio of their linear momentum ?
View SolutionThe coefficient of viscosity of a liquid of σ=1.0CGS units as determined by measuring the terminal velocity of a spherical solid ball of density p=1.5CGS units inside the liquid. If the ball of radius 1.00cm attain terminal velocity 1cm/s, then the viscosity (in CGS units) of the liquid as calculated from the observations of the experimental is: [Take g=10m/s2 ]
View Solution
