A metal disc of radius R=25cm rotates with a constant angular velocity ω=130rads^(-1)aboutitsaξs.F∈dthepotentiald⇔erencebetweenthecenterandrimofthediscif<br>(a)theexternalmag≠ticfieldis|e|nt,<br>(b)theexternaluniformmeg≠ticfieldB = 5.0mT directed perpendicular to the disc.
(a) Centripetal force required for circular motion of electron is generated by a radial electric field caused by the redis- tribution of the electrons in the disc.
F=eE=mrω2→E=mrω2e
From dV=−mω2erdr
rarr ∫v2v1dV=−mω2e∫R0rdr
V−(1)−V2=mω2R22e=(9.1×10−31)(130)2(0.25)2(2)(1.6×10−19)
=3.0×10−9V=3.0nV
V1>V2, i.e., potential at center is more than the potential at edge.
(b) A disc may be assumed to be made up of a large number of radial, conducting, differential elements rotating with angualr velocity ω about the center of disc O. This ,
Vcenter−Ved≥=12BR2ω
Now, Vcenter>Vedge for anticlockwise rotation and Vegde>Vcenter for clockwise rotation.
(a) 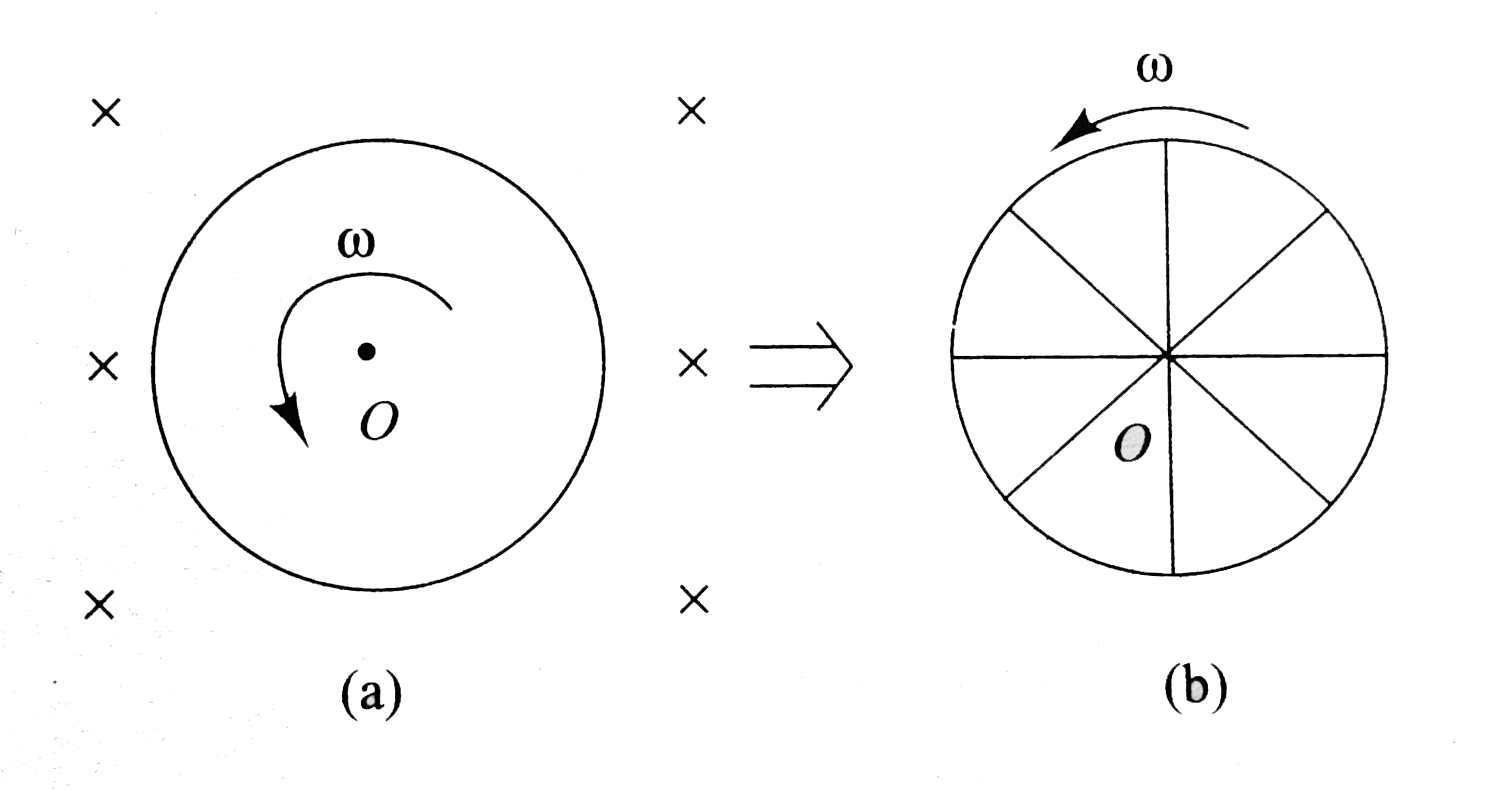
Substituting the values, we have
Vcenter−Ved≥=12×5.0×10−3×0.25×0.25×130
=0.02V=20mV
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A circular disc of radius 20 cm is rotating with a constant angular speed of 2.0rad/s in a uniform magnetic field of 0.2 T. Find the e.m.f. induced between the centre and rim of the disc. Given magnetic field is along the axis of rotation of disc.
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
Knowledge Check
A metal disc of radius a rotates with a constant angular velocity ω about its axis. The potential difference between the center and the rim of the disc is (m = mass of electron, e = charge on electro)
Amω2a2eB12mω2a2eC( c) eω2a22mDeω2a2ma conducting disc of radius R roatates about its axis when an angular velocity ω.Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
AzeroBmeω2R22eCmeω2R23eDemeω2R22An electron revolves along a circular path of radius 20 cm with constant angular velocity 120 rad s−1 about an axis passing through the centre and perpendicular to the plane of the circle. If the external magnetic field is absent, then the potential difference between the centre of the circle is (Mass of the electron =9.1×10−31 kg)
A3.691×10−9VB1.738×10−9VC4.278×10−9VD2.347×10−9V
A disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA metal disc of radius 100 cm is rotated at a constant angular speed of 60rads−1 in a plane at right angles to an external field of magnetic induction 0.05wbm−2 The emf induced between the centre and a point on the rim will be
View SolutionA metal disc of radius 100 cm is rotated at a constant angular speed of 60rads−1 in a plane at right angles to an external field of magnetic induction 0.05wbm−2 The emf induced between the centre and a point on the rim will be
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View Solution
